Калибровка моделей: зачем и как?

Медицинская прогнозная аналитика на основе большого количества данных, использующая алгоритмы машинного обучения или искусственного интеллекта приобретает всю большую популярность. Создаваемые модели оценивают риск возникновения заболеваний или состояние здоровья в будущем (« целевое событие»). Эти прогнозы могут быть учтены при принятии клинических решений и для лучшего информирования пациентов.

Алгоритмы (или модели прогнозирования риска) должны давать более высокие оценки риска для пациентов с целевым событием, чем для пациентов без события («разграничение», discrimination). Как правило, качество разграничения количественно оценивают с использованием площади под ROC-кривой (Receiver Operating Characteristic - рабочая характеристика приемника) (AUROC или AUC), также известной как статистика соответствия или c-статистика.

Кроме того, желательно указывать эффективность дихотомической классификации при одном или нескольких пороговых значениях риска, таких как чувствительность, специфичность и (специфические для подгрупп) отношения правдоподобия (sensitivity, specificity, and (stratum-specific) likelihood ratios).

Калибровка - ключевой аспект практического применения моделей, который часто упускается из виду.

Разграничение важно, но надежны ли оценки риска?

Часто упускается из виду, что прогнозы рисков могут не отражать действительные риски, даже если у прогнозных моделей хорошее разграничение. Например, оценки риска могут быть систематически завышены для всех пациентов, независимо от того, пережили они конкретное событие или нет.

Точность значений оценок риска, связанная с соответствием между предполагаемым и наблюдаемым числом событий, называется «калибровкой».

Систематические обзоры показали, что калибровка оценивается гораздо реже, чем качество разграничения, что проблематично, поскольку плохая калибровка может сделать прогнозы ошибочными. Ранее полученные результаты показали, что использование любых типов алгоритмов, от регрессии до гибких подходов машинного обучения, может привести к созданию прогнозных моделей, чья практическая ценность минимальна из-за плохой калибровки. Поэтому калибровку называют «ахиллесовой пятой» прогнозной аналитики. Калибровка особенно важна, когда целью моделей является поддержка принятия клинических решений.

Как неточные прогнозы рисков могут вводить в заблуждение?

Если алгоритм используется для информирования пациентов, то плохо откалиброванные оценки риска приводят к ложным ожиданиям пациентов и медицинских работников.

Возьмем, к примеру, модель, которая предсказывает вероятность того, что экстракорпоральное оплодотворение (ЭКО) приведет к рождению живого ребенка. Ясно, что сильная переоценка или недооценка вероятности рождения делает алгоритмы клинически неприемлемыми. Например, сильное переоценивание шансов рождения после ЭКО даст ложную надежду парам, переживающим и без того напряженный и эмоциональный опыт. Проведение процедуры для пары, которая в действительности имеет благоприятный прогноз, без необходимости подвергает женщину возможным вредным побочным эффектам, например, появлению синдрома гиперстимуляции яичников.

Фактически, плохая калибровка может сделать алгоритм менее клинически полезным, чем алгоритм конкурента, который имеет более низкую AUC, но хорошо откалиброван.

В качестве примера рассмотрим модели QRISK2–2011 и NICE Framingham для прогнозирования 10-летнего риска сердечно-сосудистых заболеваний. Внешнее проверочное исследование этих моделей с участием 2 миллионов пациентов из Великобритании показало, что QRISK2–2011 был хорошо откалиброван и имел AUC 0,771, тогда как NICE Framingham переоценивал риск с AUC 0,776. При использовании традиционного порога риска в 20% для выявления пациентов с высоким риском для проведения процедуры QRISK2-2011 выберет 110 на 1000 мужчин в возрасте от 35 до 74 лет. С другой стороны, NICE Framingham отобрал бы почти в два раза больше пациентов (206 на 1000 мужчин), потому что прогнозируемый риск 20%, основанный на этой модели, фактически соответствовал более низкой частоте событий. Этот пример показывает, что переоценка риска приводит к избыточному лечению. И наоборот, недооценка ведет к недостаточному.

Почему алгоритм может давать плохо калиброванные прогнозы риска?

1.  Часто характеристики пациентов и показатели заболеваемости или распространенности сильно различаются между медицинскими центрами, регионами и странами. Когда алгоритм разрабатывается в условиях высокой заболеваемости, он может систематически давать завышенные оценки риска при использовании в обстановке, где заболеваемость ниже. Например, университетские больницы могут лечить больше пациентов с интересующим событием, чем региональные больницы; такая неоднородность потоков пациентов может повлиять на оценки риска и их калибровку. Популяции пациентов также имеют тенденцию меняться с течением времени, например, из-за изменений в правилах выдачи направлений, политике здравоохранения или подходах к лечению.
2. Второй набор причин связан с методологическими проблемами самого алгоритма, в том числе, со статистическим переобучением. Переобученные прогнозные модели фиксируют слишком много случайного шума в данных. Таким образом, при проверке на новых данных ожидается, что переобученный алгоритм продемонстрирует более низкую точность разграничения и слишком экстремальный прогноз рисков: пациенты с высоким риском события, как правило, получают завышенные прогнозы, тогда как пациенты с низким риском события, как правило, получают заниженные прогнозы. Помимо статистического переобучения, медицинские данные обычно сами по себе содержат ошибку измерения, например, экспрессия биомаркеров варьируется в зависимости от наборов для анализа, а ультразвуковое измерение васкуляризации опухоли варьируется между наблюдателями и среди разных наблюдении одного и того же наблюдателя. 

Как оценить калибровку?

Существует 4 уровня калибровки модели:

1. «Средняя калибровка» (mean calibration) - для её оценки средний прогнозируемый риск сравнивается с общей частотой событий. Когда средний прогнозируемый риск выше, чем общая частота события, алгоритм переоценивает риск в целом. И наоборот, недооценка происходит, когда наблюдаемая частота событий выше, чем средний прогнозируемый риск.
2. «Слабая калибровка» (weak calibration) означает, что в среднем модель не завышает и не занижает риск и не дает слишком экстремальных (слишком близких к 0 и 1) или скромных (слишком близких к распространенности или заболеваемости) оценок риска. Слабую калибровку можно оценить по точке пересечения и наклону калибровочной кривой (intercept и slope). Наклон калибровки оценивает разброс предполагаемых рисков и имеет целевое значение 1. Наклон < 1 предполагает, что оцененные риски слишком велики, то есть слишком высоки для пациентов с высоким риском и слишком низки для пациентов с низким риском. Наклон > 1 говорит об обратном, т. е. о том, что оценки риска слишком умеренные. Пересечение калибровки, которое является оценкой калибровки в целом, имеет целевое значение 0; отрицательные значения указывают на переоценку, тогда как положительные значения предполагают недооценку действительных рисков.
3. «Умеренная калибровка» (moderate calibration) подразумевает, что предполагаемые риски соответствуют наблюдаемым пропорциям, например, среди пациентов с предполагаемым риском 10% у 10 из 100 возникает или развивается событие. Это оценивается с помощью гибкой калибровочной кривой (curve) для отражения связи между оцененным риском (по оси x) и наблюдаемой долей событий (ось y), например, с использованием функций loess или spline. Кривая, близкая к диагонали, указывает на то, что прогнозируемые риски хорошо соответствуют наблюдаемым пропорциям.

На графике 1a,b представлены несколько теоретических калибровочных кривых, каждая из которых соответствует разным точкам пересечения и наклонам калибровки. Обратите внимание, что точка пересечения калибровки, близкая к 0, и наклон калибровки, близкий к 1, не гарантируют, что гибкая калибровочная кривая близка к диагонали. Для получения точной калибровочной кривой требуется достаточно большой размер выборки; предлагается минимум 200 пациентов с событием и 200 пациентов без, хотя необходимы дальнейшие исследования для выяснения оптимальных объемов выборки для построения калибровочной кривой, так как такие факторы, как распространенность или заболеваемость, влияют на требуемый размер выборки. В небольших наборах данных целесообразно оценивать только слабую калибровку путем вычисления точки пересечения и наклона калибровки.

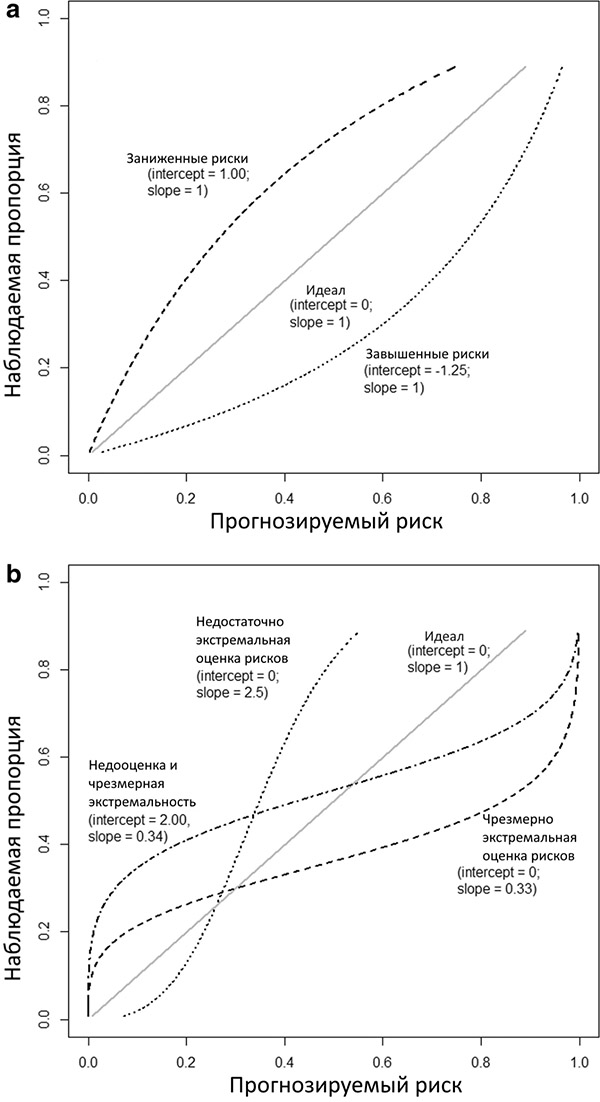
Рисунок 1. Иллюстрации различных типов неправильной калибровки.

Иллюстрации основаны на исходе с частотой событий 25% и модели с площадью под ROC-кривой (AUC или c-статистика) 0,71. Калибровочная точка пересечения и наклон указаны для каждой кривой. a Общая переоценка или недооценка прогнозируемых рисков. b Прогнозируемые риски, которые являются слишком экстремальными или недостаточно экстремальными

    4. «Сильная калибровка» (strong calibration) означает, что прогнозируемый риск соответствует наблюдаемой пропорции для каждой возможной комбинации значений предикторов; такая калибровка идеальна и является утопической целью.

Тест Хосмера-Лемешоу часто представляют как калибровочный тест, однако он имеет много недостатков: он основан на искусственном группировании пациентов по группам риска, дает неинформативное значение Р в отношении типа и степени неправильной калибровки и имеет низкую статистическую мощность.

Как предотвратить или исправить плохую калибровку?

При разработке алгоритма прогнозирования первым шагом является контроль статистического переобучения. Важно заранее определить стратегию моделирования и убедиться, что размер выборки достаточен для количества рассматриваемых предикторов.

В небольших наборах данных следует рассмотреть процедуры, направленные на предотвращение переобучения, например, с использованием методов регрессии со штрафом, таких как регрессия Риджа или Лассо или использовать более простые модели. Более простые модели могут ссылаться на меньшее количество предикторов, исключая нелинейные условия или условия взаимодействия или используя менее гибкий алгоритм (например, логистическую регрессию вместо случайных лесов или априорное ограничение количества скрытых нейронов в нейронной сети).

При внутренней проверке калибровка в целом не имеет значения, поскольку среднее значение прогнозируемых рисков будет соответствовать частоте событий. Калибровка в целом очень актуальна при внешней проверке, где часто отмечается несоответствие между прогнозируемыми и наблюдаемыми рисками.

Когда обнаруживаются плохо откалиброванные прогнозы при проверке, следует рассмотреть возможность обновления алгоритма для обеспечения более точных прогнозов для новых пациентов из проверочной выборки. Актуализация алгоритмов на основе регрессии может начаться с изменения точки пересечения для правильной калибровки в целом. Полная переделка алгоритма, как в приведенном ниже примере, улучшит калибровку, если проверочная выборка относительно велика. Стратегии непрерывного обучения алгоритмов также набирают популярность; они динамически учитывают изменения в целевой популяции с течением времени.

Опубликованное клиническое исследование по диагностике обструктивного коронарного атеросклероза:

Рассматривается модель логистической регрессии для прогнозирования обструктивного коронарного атеросклероза у пациентов со стабильной болью в груди и без обструктивного коронарного атеросклероза в анамнезе. Модель была разработана на данных 5677 пациентов, набранных в 18 европейских и американских центрах, из которых 31% имели обструктивный коронарный атеросклероз. Алгоритм был валидирован на данных 4888 пациентов в Инсбруке, Австрия, у 44% из которых был обструктивный коронарный атеросклероз. Алгоритм показал AUC 0,69.

Калибровка алгоритма выявила комбинацию завышенных (пересечение − 1,04) и чрезмерно экстремальных прогнозов риска (наклон 0,63) (Рисунок 2a). Калибровка была улучшена за счет повторного обучения (refitting) модели, т. е. путем переоценки коэффициентов предикторов (Рис. 2b).

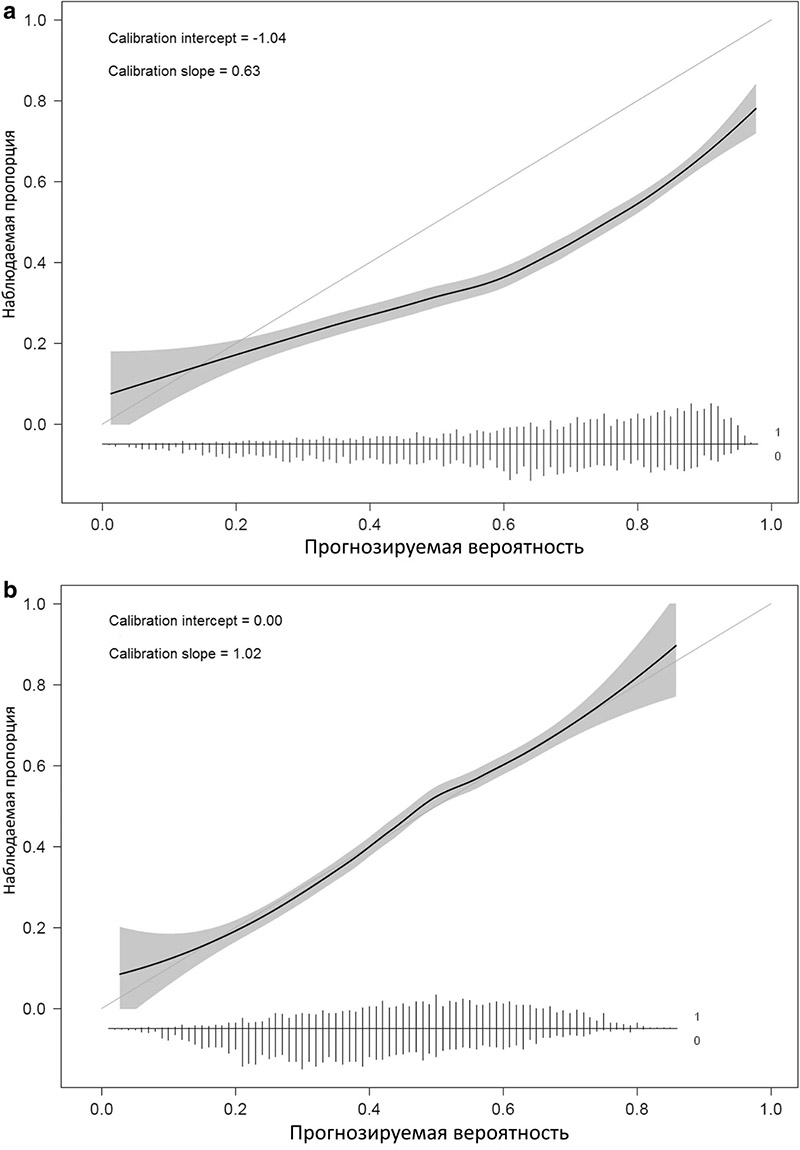
Рисунок 2

Калибровочные кривые при валидации модели обструктивного коронарного атеросклероза до и после обновления. a Калибровочная кривая перед обновлением. b Калибровочная кривая после обновления путем переоценки коэффициентов модели. Гибкая кривая с точечными доверительными интервалами (серая область) основана на локальной регрессии (loess). В нижней части графиков представлены гистограммы прогнозируемых рисков для пациентов с (1) и пациентов без обструктивного коронарного атеросклероза. Рисунок адаптирован из Edlinger et al., который был опубликован под лицензией Creative Commons Attribution – Noncommercial (CC BY-NC 4.0).

Плохо откалиброванные прогнозные модели могут вводить в заблуждение, что может привести к неправильным и потенциально опасным клиническим решениям. Следовательно, нужны заранее определенные стратегии моделирования и калибровки, подходящие для доступного размера выборки. При проверке алгоритмов крайне важно оценивать калибровку с использованием соответствующих мер и визуализаций — это помогает понять, как алгоритм работает в конкретных условиях, в которых прогнозы могут быть ошибочными, и может ли алгоритм повысить свою надежность за счет дообучения.

Из-за особенностей региональных систем здравоохранения и правил выдачи направлений к специалистам вполне вероятно, что модели прогнозирования не включают все предикторы, необходимые для учета этих различий. Наряду с явлением миграции населения модели в идеале требуют постоянного мониторинга в локальных условиях, чтобы максимизировать их преимущества с течением времени. Этот аргумент станет еще более значительным с ростом популярности очень гибких алгоритмов. Конечной целью является оптимизация полезности прогнозной аналитики для совместного принятия решений и консультирования пациентов.

Выводы по калибровке моделей машинного обучения (кроме глубокого обучения)

Почему калибровка имеет значение	Решения часто основаны на оценке риске, поэтому прогноз риска должен быть надежным
	Плохая калибровка может сделать прогностическую модель клинически бесполезной или даже вредной
Причины плохой калибровки	Статистическое переобучение и ошибка измерения
	Неоднородность популяций с точки зрения характеристик пациентов, заболеваемости или распространенности заболевания, ведения пациентов и стратегии лечения
Оценка калибровки на практике	Идеальная калибровка, при которой предсказанные риски верны для каждого шаблона ковариации, утопична; не нужно к ней стремиться
	При разработке модели стоит сосредоточиться на нелинейных эффектах и условиях взаимодействия, только если размер выборки достаточно большой; небольшие размеры выборки требуют более простых стратегий моделирования или вообще не подходят для разработки модели
	Избегайте теста Хосмера-Лемешоу для оценки или подтверждения калибровки
	При внутренней проверке сосредоточьтесь на наклоне калибровки (calibration slope) как части оценки статистического переобучения
	При внешней проверке сосредоточьтесь на калибровочной кривой, точке пересечения и наклоне калибровки (curve, intercept, slope)
	В случае плохой калибровки следует рассмотреть обновление модели; полная переоценка модели требует достаточного количества данных

Калибровка моделей на основе глубоких нейронных сетей

Если нейронная сеть предсказывает, что какое-то изображение является кошкой с достоверностью (score) 0,2, вероятность того, что это предсказание будет правильным, составляет 20%, если нейронная сеть правильно откалибрована. Такие откалиброванные оценки достоверности важны в различных прикладных задачах, где цена ошибочного предсказания велика (например, самоуправляемые автомобили, медицинская диагностика и т. д.).

Таким образом, даже если выходные данные глубокой нейронной сети еще не могут быть полностью объяснены, калибровка достоверности дает практический способ избежать серьезных ошибок на практике, связывая каждый прогноз с точной оценкой неопределенности/достоверности.

Возможные применения:

1. Фильтрация плохих прогнозов
2. Активное обучение с учетом модели
3. Обнаружение данных вне распределения обучающего набора данных

Методы оценки калибровки глубоких нейронных сетей

1. Brier Score

Оценка Брайера (BS) — это правило оценки, измеряющее квадрат ошибки между предсказанным вектором вероятности и истинной меткой, закодированной прямым унитарным кодом. Более низкие баллы соответствуют более точной калибровке. Интуитивно BS измеряет точность предсказанных вероятностей. Его можно разложить на три компонента — неопределенность, разрешение и надежность.Хотя BS является хорошей метрикой для измерения калибровки прогнозов модели, она нечувствительна к вероятностям, связанным с нечастыми событиями. Таким образом, полезно использование нескольких показателей в дополнение к BS для оценки калибровки.

2. Ожидаемая (ECE) и максимальная (MCE) ошибка калибровки

Ожидаемая ошибка калибровки (ECE) и максимальная ошибки калибровки (MCE) вычисляет разницу в ожидании между достоверностью и точностью.Как для ECE, так и для MCE более низкие баллы соответствуют более точным прогнозам. MCE обычно используется в случаях, где абсолютно необходимы надежные меры достоверности (т. е. большие ошибки в калибровке вредны), в то время как ECE обеспечивает более целостную иусредненную метрику.

3. Диаграммы надежности.

Точность отображается по оси ординат, а средняя достоверность — по оси абсцисс. Затем средние показатели достоверности и точности в каждом интервале наносятся на диаграмму, образуя линейный график. Здесь идеальная калибровка дала бы диагональную линию на диаграмме надежности.

4. Negative Log-Likelihood

Отрицательное логарифмическое правдоподобие (NLL) можно использовать для оценки неопределенности модели по сравнению с контрольными данными, где более низкие оценки соответствуют лучшей калибровке. Хотя NLL обычно используется в качестве целевой функции для обучения, NLL характеризует несоответствие между прогнозируемой и фактической достоверностью для истинной метки, достигая нулевой идеальной оценки, когда все данные прогнозируются правильно со 100% достоверностью.

5. Энтропия

Для оценки поведения модели на данных из другого распределения по сравнению с обучающей выборкой ни одна из предыдущих метрик не может быть использована из-за отсутствия истинной разметки. Вместо этого поведение модели обычно анализируется путем измерения энтропии выходного распределения, создаваемого данными вне распределения. Выходные распределения с высокой и низкой энтропией. Интуитивно, данные вне распределения должны приводить к сетевым прогнозам с высокой энтропией, соответствующей состоянию неопределенности, в котором всем возможным выходным данным назначается одинаковая вероятность. С другой стороны, сетевые прогнозы для хорошо понятных данных должны иметь низкую энтропию, поскольку модель прогнозирует правильный класс с высокой степенью достоверности, если она точна и правильно откалибрована.

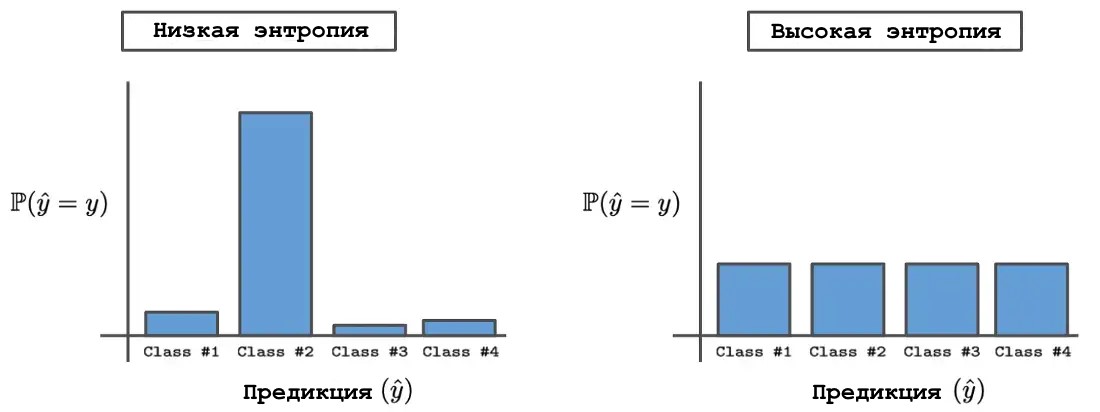
Выходные распределения с высокой и низкой энтропией

Методы калибровки

1.Температурная шкала

Настройка температуры softmax выходного для минимизации NLL в валидационном наборе наиболее эффективна при калибровке сетевых прогнозов. Таким образом, преобразование softmax модифицируется, как показано ниже, с положительной температурой T.

 
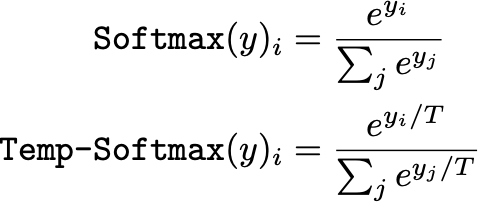
Преобразование Softmax с температурной шкалой и без нее

В этом выражении большие значения T будут «смягчать» выходное распределение (т. е. смещать его к равномерному распределению), в то время как меньшие значения T будут уделять больше внимания выходным данным с наибольшим значением в распределении. Таким образом, параметр T существенно контролирует энтропию выходного распределения.

Настраивая параметр T по набору проверочных данных для оптимизации NLL, можно значительно улучшить калибровку сети. Однако этот процесс калибровки требует набора данных проверки и выполняется как отдельный этап после обучения. Также было обнаружено, что этот метод плохо работает для обработки данных вне распределения и совсем не работает для данных, не являющихся независивыми и одинаково распределёнными.

2. Калибровка на основе ансамбля (Ensemble-based)

Ансамбли — группы из нескольких независимо обученных сетей, которые используются совместно для прогнозирования — широко известны тем, что обеспечивают улучшенную производительность по сравнению с отдельными сетями. Усреднение прогнозов сетей в ансамбле также может быть использовано для получения полезных оценок неопределенности.
 
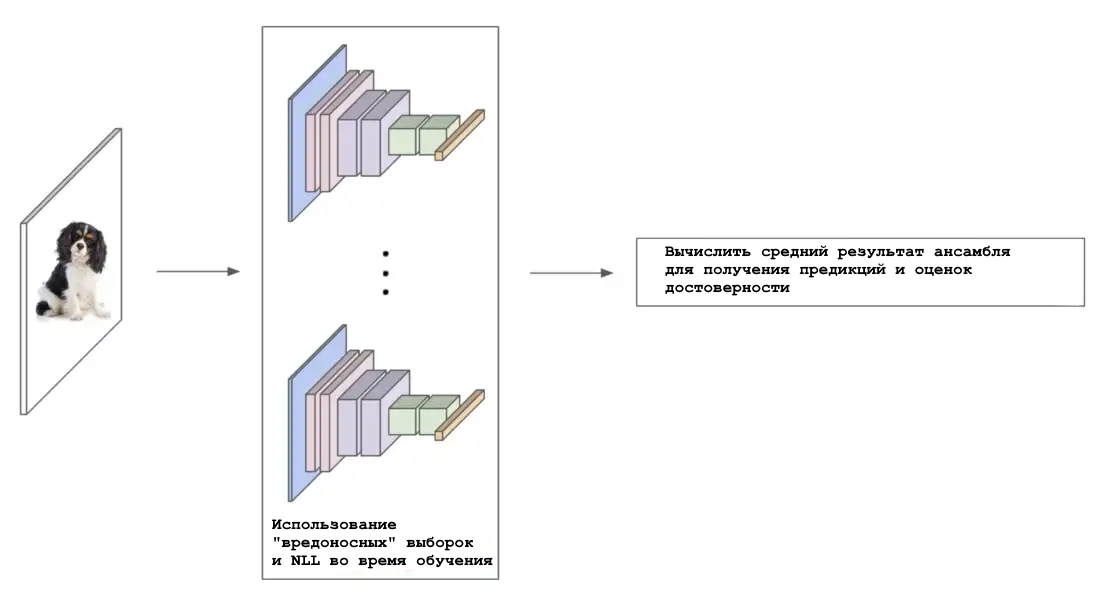
Обзор ансамблевой калибровки

Каждая сеть в ансамбле обучается независимо и на полном наборе данных (т. е. с различной случайной инициализацией и перетасовкой). Затем, усредняя прогнозы полученного ансамбля, можно получить качественные оценки неопределенности даже на больших наборах данных. Кроме того, показано, что такой подход устойчив к сдвигам в наборе данных. Таким образом, методы калибровки на основе ансамбля, несмотря на дополнительные вычислительные затраты на работу с несколькими сетями, являются простыми, надежными и производительными.

3. Mixup

Mixup — это простой метод увеличения данных, который берет выпуклые комбинации обучающих примеров со случайно выбранными (из бета-распределения) взвешиваниями и использует такие комбинированные выборки для обучения сети.

 
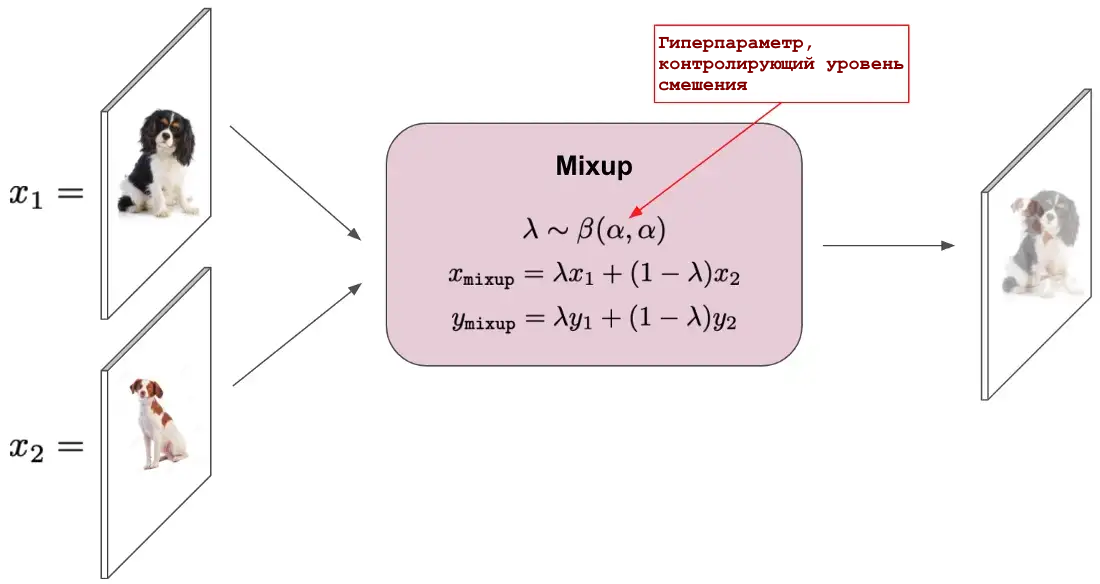
Процедура увеличения данных Mixup

Примечательно, что mixup использует комбинацию как входных изображений, так и связанных с ними меток. Использование mixup во время обучения, помимо обеспечения значительных преимуществ в регулировании и производительности, может привести к моделям классификации с улучшенными калибровочными свойствами. Mixup также показал свою эффективность при обнаружении данных вне распределения.

4. Байесовские нейронные сети

Байесовские нейронные сети основаны на том, что бесконечно широкие нейронные сети с распределениями по их весам сходятся к гауссовским процессам.

Байесовские нейронные сети - это конечные нейронные сети с распределениями, размещенными по их весам. Они требуют непомерно высоких вычислительных ресурсов и памяти. Размер базовой модели обычно должен быть удвоен, чтобы можно было правильно оценить неопределенность с помощью байесовской формулы.

5. Drop-out как байесовская аппроксимация (Dropout as a Bayesian Approximation)

Нейронные сети, обученные с drop-out, представляют собой байесовскую аппроксимацию гауссовских процессов. Этот метод обычно методологии, которую обычно называют drop-out по методу Монте-Карло.

 
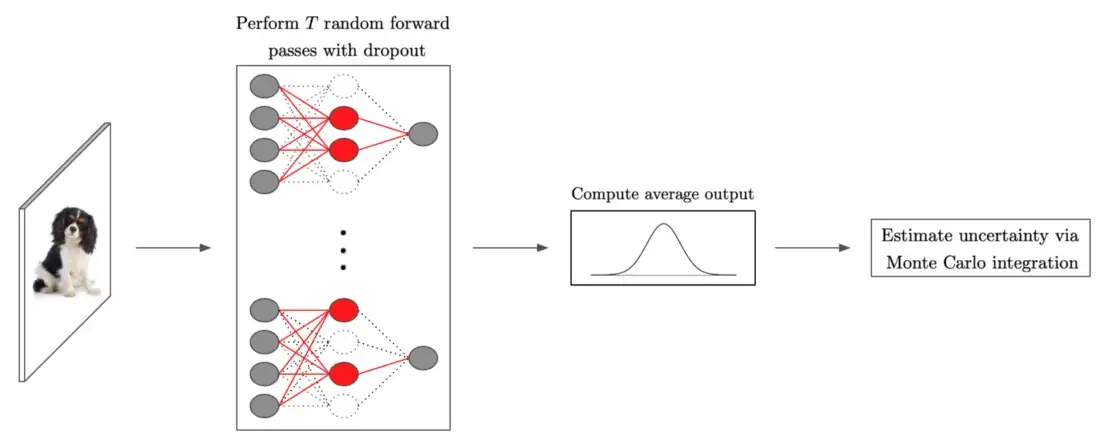
Оценка неопределенности с drop-out

Все, что требуется, — это обучить обычную сеть с drop-out и выполнить несколько случайных прямых проходов с drop-out во время тестирования, где каждый из них можно распараллелить, чтобы избежать дополнительной задержки. Такой подход годится для широкомасштабного использования, и обеспечивает как хорошую калибровку, так и обнаружение данных вне распределения с высокой точностью. Однако производительность калибровки на основе дропаута немного хуже, чем у рассмотренных выше методов на основе ансамбля.

Пост подготовлен на основе статей:

1.    Van Calster, B., McLernon, D.J., van Smeden, M. et al. Calibration: the Achilles heel of predictive analytics. BMC Med 17, 230 (2019). https://doi.org/10.1186/s12916-019-1466-7. URL https://bmcmedicine.biomedcentral.com/articles/10.1186/s12916-019-1466-7
2.    https://towardsdatascience.com/confidence-calibration-for-deep-networks-why-and-how-e2cd4fe4a086