
В каждой задаче машинного обучения ставится вопрос оценки результатов моделей.
Без введенных критериев, невозможно будет ни оценить “успешность” модели, ни сравнить между собой два различных алгоритма. Именно поэтому важно учесть правильный выбор метрик для поставленной задачи, хотя множество существующих метрик может запутать и, в конечном счете, привести к неоптимальному решению.
Несмотря на популярность машинного обучения, во многих её сферах до сих пор не сформировалась единая теоретическая концепция. Исключением не стала и рассматриваемая область. Хоть и существуют некоторые общие рекомендации к применению метрик для некоторых задач, конечное решение лежит на плечах аналитика.
Бинарная классификация
Знакомство с этим фундаментальным разделом стоит начать с изучения способов оценки одной из наиболее популярной постановки задачи - бинарной классификации. В данном случае, данные поделены всего на два класса. Их метки принято обозначать как «+» и «-». Рассматриваемые нами метрики основаны на использовании следующих исходов: истинно положительные (TP), истинно отрицательные (TN), ложно положительные (FP) и ложно отрицательные (FN). Для наглядности, можно преобразовать в таблицу сопряженности (Рисунок 1). Ложно положительный и ложно отрицательный исход ещё называют ошибками первого и второго рода соответственно.
Возьмём, к примеру задачу выявления подозрения на определенное заболевание. Если у пациента оно есть, то это будет положительным классом. Если нет – отрицательным. Результатом работы модели может быть определение – следует ли «заподозрить» у пациента какой-то определенный диагноз (тогда результат = true) или нет (тогда результат = false).
Пусть какой-то набор медицинских данных характерен для данного диагноза. Если наша модель верно определила и поставила положительный класс, тогда это истинно положительный исход, если же модель ставит отрицательную метку класса, тогда это ложно отрицательный исход. В случае отсутствия диагноза у рассматриваемого набора данных исходы модели остаются аналогичными. Тогда если модель относит запись к классу положительную, то мы говорим о ложно положительном исходе (модель «сказала» что диагноз есть, но на самом деле его нет), и наоборот, если модель определят запись как отрицательный класс, то это — истинно отрицательный исход.
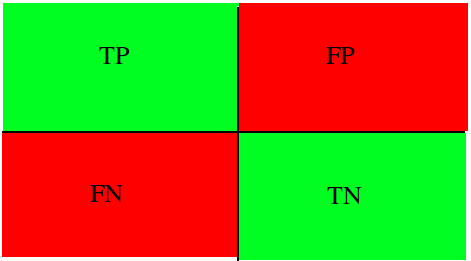
Рисунок 1: Матрица сопряженности возможных результатов бинарной классификации
Accuracy
Одной из наиболее простых, а поэтому и распространенной метрикой является точность. Она показывает количество правильно проставленных меток класса (истинно положительных и истинно отрицательных) от общего количества данных и считается следующим образом [Evaluation: from precision, recall and F-measure to ROC, informedness, markedness and correlation]:
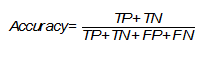
Однако, эта простота является также и причиной, почему её часто критикуют и почему она может абсолютно не подойти под решаемую задачу. Она не учитывает соотношения ложных срабатываний модели, что может быть критическим, особенно в медицинской сфере, когда стоит задача распознать все истинные случаи диагноза.
Вернемся к примеру с подозрением на заболевание. Если наша точность равна 80%, то можно сказать, что в среднем из 100 человек она правильно определит наличие или отсутствие диагноза лишь у 80 человек, тогда как ещё 20 будут либо ложно отрицательными, либо ложно положительными.
Стоит обратить внимание на то, что в некоторых задачах необходимо определить всех пациентов с диагнозом и можно даже пренебречь ложно положительными исходами, так как они могут отсеяться на следующих стадиях исследования (например, после контрольной сдачи анализов), тогда необходимо добавить к этой метрике ещё одну, которая могла бы оценить требуемый приоритет.
Precision
Несмотря на различные английские названия и разные формулы подсчета, русский перевод этой метрики также закрепился как «точность», что может вызвать недоумение и конфуз, поэтому следует уточнять, о чем именно вы говорите. Эта точность показывает количество истинно положительных исходов из всего набора положительных меток и считается по следующей формуле [Evaluation: from precision, recall and F-measure to ROC, informedness, markedness and correlation]:
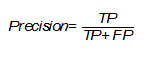
Важность этой метрики определяется тем, насколько высока для рассматриваемой задачи «цена» ложно положительного результата. Если, например, стоимость дальнейшей проверки наличия заболевания у пациента высока и мы просто не можем проверить все ложно положительные результаты, то стоит максимизировать данную метрику, ведь при Precision = 50% из 100 положительно определенных больных диагноз будут иметь лишь 50 из них.
Recall (true positive rate)
В русском языке для этого термина используется слово «полнота» или «чувствительность». Эта метрика определяет количество истинно положительных среди всех меток класса, которые были определены как «положительный» и вычисляется по следующей формуле [The relationship between Precision-Recall and ROC curves ].
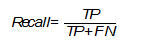
Необходимо уделить особое внимание этой оценке, когда в поставленной задаче ошибка нераспознания положительного класса высока, например, при выставлении диагноза какой-либо смертельной болезни.
F1-Score
В том случае, если Precision и Recall являются одинаково значимыми, можно использовать их среднее гармоническое для получения оценки результатов [On extending f-measure and g-mean metrics to multi-class problems]:
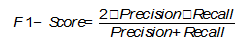
Помимо точечных оценок, существует целый ряд графических методов, способных оценить качество классификации.
ROC
ROC (receiver operating characteristic) – график, показывающий зависимость верно классифицируемых объектов положительного класса от ложно положительно классифицируемых объектов негативного класса. Иными словами, соотношение True Positive Rate (Recall) и False Positive Rate (Рисунок 2). При этом, False Positive Rate (FPR) рассчитывается по следующей формуле [Evaluation: from precision, recall and F-measure to ROC, informedness, markedness and correlation]:
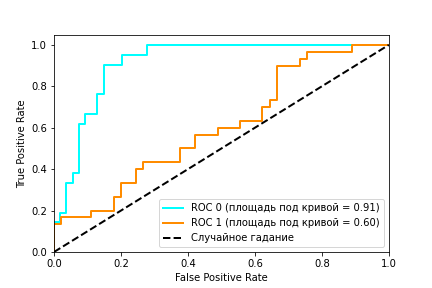
Рисунок 2: ROC кривая
Рисунок 2 содержит пример двух ROC – кривых. Идеальное значение графика находится в верхней левой точке (TPR = 1, a FPR = 0). При этом, кривая, соответствующая FPR = TPR является случайным гаданием, а если график кривой модели или точка находятся ниже этого минимума, то это говорит лишь о том, что лучше подбрасывать монетку, чем использовать эту модель. При этом говорят, что кривая X доминирует над другой кривой Y, если X в любом точке находится левее и выше Y [Using AUC and accuracy in evaluating learning algorithms ], что означает превосходство первого классификатора над вторым.
С помощью ROC — кривой, можно сравнить модели, а также их параметры для поиска наиболее оптимальной (с точки зрения tpr и fpr) комбинации. В этом случае ищется компромисс между количеством больных, метка которых была правильно определена как положительная и количеством больных, метка которых была неправильно определена как положительная.
AUC (Area Under Curve)
В качестве численной оценки ROC кривой принято брать площадь под этой кривой, которая является неплохим «итогом» для кривой. Если между кривыми X и Y существует доминирование первой над второй, то AUC (X) > AUC (Y), обратное не всегда верно. Но AUC обладает так же и статистическим смыслом: она показывает вероятность того, что случайно выбранный экземпляр негативного класса будет иметь меньше вероятность быть распознанным как позитивный класс, чем случайно выбранный позитивный класс [Using AUC and accuracy in evaluating learning algorithms].
AUC часто сравнивают с метрикой Accuracy и у первой есть явное преимущество при исследовании некоторых моделей - она может работать с вероятностями. Например, в AUC: a better measure than accuracy in comparing learning algorithms показан следующий пример (Рисунок 3): пусть две модели классифицируют 10 тестовых экземпляров. 5 они классифицируют как положительный класс и столько же как отрицательный, так же экземпляры упорядочены в соответствии с вероятностью принадлежать положительному классу (слева — направо). Оба классификатора имеют одинаковую точность — 80%, но AUC у первого — 0.96, а у второго — 0.64, поскольку вероятности ошибочных экземпляров разная. Но так же можно найти и контрпример, когда AUC одинаковый, а точность разная [ AUC: a better measure than accuracy in comparing learning algorithms].

Рисунок 3.Два классификатора имеют одинаковую точность, но разный AUC
Мульти-классификация
Все рассмотренные выше метрики относились лишь к бинарной задаче, но, зачастую, классов больше, чем два. Это обуславливает необходимость в обобщении рассмотренных метрик. Одним из возможных способов является вычисление среднего метрики по всем классам [On extending f-measure and g-mean metrics to multi-class problems]. Тогда в качестве «положительного» класса берется вычисляемый, а все остальные — в качестве «отрицательного».
В этом случае формулы для метрик будут выглядеть следующим образом:

Применение в предиктивной аналитике для здравоохранения
Изученную теорию всегда следует подкрепить практикой. В данном случае, можно рассмотреть применение тех или иных метрик для реальных задач, связанных с использованием моделей машинного обучения в здравоохранении. В большинстве случаев рекомендуется использовать метрики AUC и F-Score, потому что они включают в себя широкий список возможных исходов и, как было замечено ранее, AUC превосходит метрику Accuracy, но спор насчет этого ведётся до сих пор.
Основной задачей предиктивной аналитики для здравоохранения является предсказание различных событий. Эта тема довольно неплохо изучена для различных заболеваний и сценариев использования, поэтому существует множество возможных методов её решения. Данный тип задач оценивается всеми рассмотренными метриками для классификации, но чаще остальных можно заметить Accuracy благодаря её простоте. Например, в Disease prediction by machine learning over big data from healthcare communities авторы анализируют медицинские записи с целью предсказания возможности появления какого-либо заболевания и у них получается это на уровне 70% для Accuracy, Precision, Recall и F1. В Intelligent heart disease prediction system using data mining techniques и Heart disease prediction system using naive Bayes метрика Accuracy достигает приблизительно 90-95%, но на это сказывается размер набора данных, который был использован для исследования.
Среди всего списка заболеваний особую актуальность имеют сердечно сосудистые заболевания (ССЗ). Множество исследований, посвященных предсказанию ССЗ демонстрируют то, чего можно достичь в этой области благодаря машинному обучению. Зачастую здесь используется метрика AUC для сравнения качества моделей. Например в A data-driven approach to predicting diabetes and cardiovascular disease with machine learning авторы работали с базой, которая собиралась в течение 20 лет, содержащей более ста признаков. Целью являлось предсказание ранних стадий ССЗ, предиабета и диабета, они добились показателей равных 0.957, 0.802 и 0.839 площади под кривой. В Development and verification of prediction models for preventing cardiovascular diseases авторы исследовали возможность различных исходов (смерть, госпитализация и другие), связанных с ССЗ. Наилучший показатель AUC был равен 0.96. В Перспективы использования методов машинного обучения для предсказания сердечно-сосудистых заболеваний исследуется возможность предсказания ССЗ с помощью методов машинного обучения и некоторых медицинских данных. Для Accuracy, Precision, Recall и AUC были получены результаты 78%, 0.79, 0.67 и 0.84 соответственно.
Заключение
Рассмотренные метрики являются лишь основными и только для задачи классификации. Существует ещё множество различных областей, в которых они будут разными, потому что каждая задача имеют свою специфику и приоритеты. Невозможно дать каких-то четких гарантий и определить, какая из метрик лучше, выбирать и отдавать предпочтение стоит лишь исходя из опыта своего и других исследователей.