Метрики качества работы моделей машинного обучения: как их понимать и использовать?

Введение

Системы искусственного интеллекта (СИИ) для клинической медицины в подавляющем большинстве случаев создаются на основе различных моделей машинного обучения (ММО). Задача этих моделей состоит в интерпретации медицинских данных: радиологических изображений, врачебных записей в электронных медицинских картах, видео- или звуковых файлах и т.д. для ответа на определенный вопрос, как правило – либо о наличии признаков какого-то заболевания, либо для прогнозирования различных событий.

Одной из ключевых задач, с которой сталкиваются как разработчики соответствующих систем, так и затем эксперты и лица, принимающие решения о допуске продуктов на рынок или их практическом внедрении – является задача оценки качества СИИ, которая, соответственно, сводится к оценке качества модели машинного обучения, включенной в продукт.

В настоящее время действует несколько различных стандартов, описывающих метрики и методы оценки качества СИИ для здравоохранения, например ГОСТ Р 71673-2024, ГОСТ Р 59921.7-2022, ПНСТ 872-2023, ГОСТ Р 59921.9-2022 и ГОСТ Р 59921.1-2022.

Кроме этого, имеются различные методические рекомендации, в которых рассматриваются вопросы метрик качества моделей машинного обучения и их оценки для применения в условиях реальной клинической практики.

Наконец, в сфере научных исследований и клинических испытаний моделей машинного обучения (ММО) для медицины также создан целый комплекс методик и подходов к обеспечению единства и доверия к таким результатам.

Таким образом, мы имеем довольно приличный набор готовых методических документов и требований, которыми необходимо оперировать при оценке качества ММО. Их большое количество и, подчас, сложность и противоречивость создают серьезную проблему и даже споры о том, как же на самом деле следует оценивать качество работы ММО, причем как среди экспертов, так и среди компаний-разработчиков и пользователей СИИ.

В этой связи мы в Webiomed решили обобщить все доступные стандарты и рекомендации относительно метрик качества работы моделей машинного обучения с точки зрения их применимости в практическом здравоохранении и представить в едином описании, снабдив все не просто формулами и формальными названиями метрик, но и пояснениями – что каждая из этих метрик означает и как ее следует интерпретировать.

Общие сведения о тестировании модели

В общем виде каждая модель машинного обучения, встроенная в СИИ, принимает на вход определенные медицинские данные, чаще всего в обезличенном виде, анализирует и интерпретирует эти данные и возвращает результат такой обработки, который затем уже используется программным кодом СИИ и в конечном счете выводится в пользовательском интерфейсе.

В основе любой оценки качества работы ММО, будь то внутреннее тестирование на этапах разработки или внешняя клиническая валидация на этапе подготовки к государственной регистрации в качестве медицинского изделия, лежит метод сравнения ответов, что вернула модель, с некоторыми эталонными значениями, представленными в специально подготовленном для тестирования наборе данных.

Если речь идет о внутреннем тестировании – то, как правило, это часть обучающего набора, которая случайным образом извлечена из него и помещена в тестовый набор данных, при этом записи из такого набора не участвуют в обучении модели. Такой набор данных обычно называют тестовым.

Если речь идет о внешней клинической валидации, то здесь используется набор данных, подготовленный независимо от сотрудников компании-разработчика СИИ, а также из данных, которые не были доступны разработчику во время создания или внутреннего тестирования модели. Его называют валидационным.

В любом случае набор данных содержит входные данные для проверки модели (изображения, текстовые документы или извлеченные из них признаки и т.д.) и сопоставленные ним правильные ответы (выходные данные, которые мы ожидаем получить от модели).

Соответственно, при проведении тестирования (или внешней валидации) из набора данных берутся содержащиеся там записи, из каждой записи – берутся входные данные и отправляются для интерпретации в модель, которая обрабатывает их и возвращает результат интерпретации. Полученный результат записывается в тестовый набор данных. В результате в нем получается 2 пары ответов – эталонный (правильный, фактический) и полученный от модели (предсказанный).

После завершения теста (обработки записей тестового или валидационного набора данных) мы получаем в наборе по каждой строке соответствующее ей 2 пары ответов. Используя эти результаты, далее выполняется расчет метрик качества работы модели, в основе которых лежит так называемая «матрица ошибок» (confusion matrix).

Что такое матрица ошибок

Рассмотрим самую простую и распространённую ситуацию, когда модель на основе интерпретации поданных в нее данных должна вернуть оценку – относится ли пациент к какой-то искомой группе или нет? Ответ на такой вопрос называется решением задачи классификации.

Обратим внимание, что такой ответ модели может быть востребован как в диагностике заболеваний, так и в прогнозировании различных событий.

Пример из диагностики: модель должна выполнить анализ рентгенограммы для определения – есть ли у пациента патология на снимке или нет? В этом случае модель вернет ответ, что пациент либо относится к группе больных (обычно такую группу называют «Класс 1»), либо он относится к группе здоровых («Класс 0»).

Пример из прогностики: модель должна выполнить анализ записи в электронной медкарте для определения группы риска пациента относительно возможной смерти в течении 1 года. В этом случае модель вернет ответ, что пациент либо относится к «Высокому риску» («Класс 1»), либо к низкому риску («Класс 0»).

В обоих рассматриваемых ситуациях ответом модели будет так называемый бинарный отклик. Это означает, что ответ модели может быть либо True (пациент относится к «Классу 1»), либо False (пациент относится к «Классу 0»).

Соответственно, для того чтобы корректно проверить работу такой модели, подготовленный для тестирования набор данных также должен содержать ожидаемые (правильные, эталонные) ответы по каждой записи набора – либо True («Класс 1»), либо False («Класс 0»).

Всегда существует ненулевая вероятность того, что модель машинного обучения ошибается при обработке поданных в нее данных. Это означает, что при сравнении полученного ответа модели с правильным, мы можем получить один из 4 возможных вариантов:

1. Истинно положительный результат (ИП, True Positives): модель правильно определила Класс 1. Пример из диагностики – модель у больного пациента правильно определила, что он больной. Прогностика – модель правильно предсказала что у пациента случится смертельный исход – он действительно случился в пределах прогнозируемого периода.
2. Истинно отрицательный результат (ИО, True Negative): модель правильно определила Класс 0. У здорового человека модель правильно вернула ответ False на вопрос о наличии патологии в рентгенограмме, или она правильно предсказала что смерти не будет в задаче прогностики.
3. Ложноположительный результат (ЛП, False Positives): модель неправильно определила класс 1. На самом деле это был здоровый пациент, у которого нет патологических признаков в рентгенограмме или модель предсказала смерть у пациента, у которого ее не случилось.
4. Ложноотрицательный результат (ЛО, False Negatives): модель неправильно определила класс 0. Это был больной пациент, но модель определила его как здорового. В задаче прогностики – модель отнесла пациента к низкому риску, хотя на самом деле пациент умер.

Соответственно, проведя тестирование модели на всем числе записей из тестового набора данных, мы можем рассчитать – сколько из полученных от модели ответов были отнесены к этим 4 вариантам.

Визуальное отображение полученных результатов и называется матрицей ошибок. Обратим внимание, что она может быть рассчитана как для бинарной, так и для многоклассовой классификации.

В случае бинарной классификации матрица ошибок представляет собой таблицу, состоящую из двух строк и двух столбцов, при этом строки соответствуют фактическим классам, а столбцы — ответам модели.

	Класс 1 (ответ модели)	Класс 0 (ответ модели)
Класс 1 (правильный ответ)	ИП Модель выявила патологию при ее наличии	ЛП Модель выявила патологию при ее отсутствии
Класс 0 (правильный ответ)	ЛО Модель не выявила патологию при ее наличии	ИО Модель не выявила патологию при ее отсутствии

Если ячейка матрицы ошибок расположена на пересечении строки и столбца для одного и того же класса (т.е. элемент на главной диагонали), то она соответствует истинным классификациям, и в ней ставится число правильно обработанных примеров для соответствующего класса. Если столбец и строка, на пересечении которых расположена ячейка, относятся к разным классам, то в ней окажется число ошибочно определенных примеров.

Полученные 4 показателя матрицы ошибок используются далее для расчета соответствующих метрик качества модели.

В общем случае при оценке качества модели на популяционном уровне используют метрики чувствительности и специфичности, а на уровне пациента большую значимость имеют прогностические ценности результатов. Данные метрики описаны детально в следующем разделе.

   I. Общие показатели (Overall performance)

Ia. Ключевые метрики для принятия управленческих решений

1. Точность (Accuracy)

Формула:     (ИП + ИО)/(ИП + ИО + ЛП + ЛО)

Описание: количество правильно интерпретированных записей в наборе данных (истинно положительных и истинно отрицательных) от общего количества записей в наборе данных. Может иметь значения от 0 до 100%.

Интерпретация:

Если точность равна 80%, то это означает, что из 100 человек она правильно определит наличие или отсутствие патологии лишь у 80 человек, тогда как ещё 20 будут либо ложно отрицательными, либо ложно положительными.

Не смотря на свою простоту и универсальность, точность имеет ряд серьёзных недостатков:

•     не учитывает дисбаланс классов: если один класс значительно преобладает над другим, то модель может быть смещена в его сторону, и тогда высокая точность не будет отражать истинное качество модели;
•     не даёт информацию о типе ошибок модели, например, о количестве ложноположительных и ложноотрицательных результатов, что не позволяет учитывать цену ошибки для разных классов;
•     зависит от порога классификации, изменение которого может значительно повлиять на значение точности.

При принятии решения о приемлемости полученной метрики с точки зрения применения модели в условиях реальной клинической практики рекомендуется использовать следующие пороговые значения [1]:

Значение	Решение
<0,6	Модель имеет неприемлемо низкую точность, ее использование в реальной практике недопустимо
0,61 - 0,8	Модель имеет перспективную точность, но требуется ее улучшение до более высокого значения
>0,81	Модель имеет приемлемую точность, ее можно использовать

2. Полнота или Чувствительность (Recall / True positive rate / Sensitivity)

Формула:     ИП/(ИП + ЛО)

Описание: Доля лиц с положительным результатом для целевой популяции с изучаемым заболеванием (т. е. вероятность того, что пациенты с наличием детектируемого моделью заболевания будут корректно выявлены с помощью модели) [2]. Показатель истинной положительности [3].

Интерпретация:

Необходимо уделить особое внимание этой оценке, когда в поставленной перед моделью задаче ошибка пропуска пациента с заболеванием высока (ошибка 1го рода), например, при выявлении опасной смертельной болезни.

В медицине чувствительность показывает, какова будет доля пациентов, у которых исследование даст положительный результат. Чем выше чувствительность теста, тем чаще с его помощью будет выявляться заболевание.

В то же время, если такой высокочувствительный тест оказывается отрицательным, то наличие заболевания маловероятно. Поэтому их следует применять для исключения заболеваний на ранних этапах диагностического процесса, когда требуется сузить круг предполагаемых заболевших. Необходимо также отметить, что высокочувствительный тест дает много «ложных тревог», что требует дополнительных затрат на дальнейшее обследование. Чувствительный тест наиболее информативен при отрицательном его результате, т.е. врач более уверен в том, что не пропустил заболевание.

При принятии решения о приемлемости полученной метрики с точки зрения применения модели в условиях реальной клинической практики рекомендуется использовать следующие пороговые значения [1]:

Значение	Решение
<0,6	Модель имеет неприемлемо низкую точность, ее использование в реальной практике недопустимо
0,61 - 0,8	Модель имеет перспективную точность, но требуется ее улучшение до более высокого значения
>0,81	Модель имеет приемлемую точность, ее можно использовать

3. Специфичность (Specificity)

Формула:     ИО/(ИО +ЛП)

Описание: Доля лиц с отрицательным результатом модели в целевой популяции без изучаемого заболевания (т. е. вероятность того, что пациенты без детектируемого заболевания будут определены как здоровые) [2]. Показатель истинной отрицательности [3].

Интерпретация:

Если число ложноположительных классификаций велико, т.е. модель допустила большое количество ошибок, распознав отрицательные примеры как положительные, то специфичность стремится к 0. Напротив, если же число ложноположительных наблюдений стремится к 0, то специфичность стремится к 1.
Модель, обладающая высокой специфичностью, обеспечивает большую вероятность правильного распознавания действительно отрицательных случаев.

В медицине определив специфичность теста, можно предполагать, какова доля здоровых лиц, у которых это исследование даст отрицательный результат. Чем выше специфичность метода, тем надежнее с его помощью подтверждается заболевание. Высокоспецифичные методы эффективны на втором этапе диагностики, когда круг предполагаемых заболеваний сужен и необходимо с большой уверенностью доказать наличие болезни. Отрицательным фактором высокоспецифичного метода диагностики является тот факт, что его использование сопровождается значительным числом пропусков заболевания. Специфичные тесты нужны для подтверждения (установления) диагноза, т.е. при положительном результате врач должен быть почти уверен в том, что не «приписал» здоровому человеку несуществующую болезнь.

При принятии решения о приемлемости полученной метрики с точки зрения применения модели в условиях реальной клинической практики рекомендуется использовать следующие пороговые значения [1]:

Значение	Решение
<0,6	Модель имеет неприемлемо низкую точность, ее использование в реальной практике недопустимо
0,61 - 0,8	Модель имеет перспективную точность, но требуется ее улучшение до более высокого значения
>0,81	Модель имеет приемлемую точность, ее можно использовать

Кроме указанных выше метрик также зачастую принимают во внимание метрику площадь под характеристической кривой (AUROC). Однако, эта метрика характеризует не точность прогнозирования модели, а ее дикриминирующую способность. В связи с этим мы включили эту метрику в раздел «Показатели дискриминации» ниже.

Ib. Ключевые метрики для принятия решений по пациенту

4. Прогностическая ценность положительного результата (ПЦПР) (Precision / Positive predictive value / PPV)

Формула:     ИП/(ИП + ЛП)

Описание: Вероятность заболевания при положительном результате СИИ [2]. Посттестовая вероятность наличия заболевания при положительном результате теста [3].

Интерпретация:

Важность этой метрики определяется тем, насколько высока для рассматриваемой задачи «цена» ложно положительного результата. Если, например, стоимость дальнейшей проверки наличия заболевания у пациента высока, и это будет слишком ресурсозатратно перепроверить все ложно положительные результаты, то стоит максимизировать данную метрику, ведь при ПЦПР = 50% из 100 положительно определенных больных, диагноз будут иметь лишь 50 из них.

Положительная прогностическая ценность возрастает по мере того, как положительный класс чаще встречается в выборке, на которой эта метрика оценивается. Кроме того, тесты с высокой специфичностью улучшают положительную прогностическую ценность. С тестами высокой специфичности меньше ложных срабатываний.

При принятии решения о приемлемости полученной метрики с точки зрения применения модели в условиях реальной клинической практики рекомендуется использовать следующие пороговые значения [1]:

Значение	Решение
<0,6	Модель имеет неприемлемо низкую точность, ее использование в реальной практике недопустимо
0,61 - 0,8	Модель имеет перспективную точность, но требуется ее улучшение до более высокого значения
>0,81	Модель имеет приемлемую точность, ее можно использовать

5. Прогностическая ценность отрицательного результата (ПЦОР) (Negative Predictive Value / NPV)

Формула:     ИО/(ИО + ЛО)

Описание: Вероятность отсутствия заболевания при отрицательном (нормальном) результате СИИ [2]. Посттестовая вероятность отсутствия заболевания при отрицательном результате теста [3].

Интерпретация:

Если тест на хламидиоз имеет 80% чувствительность и 80% специфичность в популяции из 100 человек с распространенностью хламидиоза 10%, вы можете ожидать следующее:

• 8 из 10 истинно положительных случаев дают положительный результат модели.
• 72 из 90 истинно отрицательных случаев дали отрицательный результат модели.
• Из 74 отрицательных тестов 72 являются истинно отрицательными (у них нет инфекции) и 2 - ложноотрицательными (они дали отрицательный результат, но на самом деле у них есть инфекция).

Следовательно, NPV составит 97% (72/74). Можно ожидать, что 97% людей с отрицательным результатом теста на хламидиоз будут отрицательными.

Напротив, если тот же тест проводится в популяции с распространенностью хламидиоза 40, NPV будет другим. Это потому, что NPV учитывает больше, чем просто чувствительность и специфичность диагностического теста. В таком случае:

• 32 из 40 истинно положительных случаев дают положительный результат модели.
• 48 из 60 истинно отрицательных случаев дали отрицательный результат модели.
• Из 56 отрицательных результатов тестов 8 являются ложноотрицательными. Это означает, что отрицательная прогностическая ценность составляет 85% (48/56) [4].

Тесты с высокой чувствительностью увеличивают отрицательную прогностическую ценность. Это связано с тем, что у большего числа людей с положительным результатом теста с высокой чувствительностью появляется меньше ложноотрицательных результатов.
Отрицательная прогностическая ценность снижается по мере того, как болезнь становится более распространенной среди населения.

При принятии решения о приемлемости полученной метрики с точки зрения применения модели в условиях реальной клинической практики рекомендуется использовать следующие пороговые значения [1]:

Значение	Решение
<0,6	Модель имеет неприемлемо низкую точность, ее использование в реальной практике недопустимо
0,61 - 0,8	Модель имеет перспективную точность, но требуется ее улучшение до более высокого значения
>0,81	Модель имеет приемлемую точность, ее можно использовать

Ic. Дополнительные метрики

6. Отношение правдоподобия положительного результата (Likelihood ratio for positive results / LR+)

Формула:     Чувствительность/ (1 - специфичность)

Описание: Математически отображает, во сколько раз при положительном результате СИИ вероятность наличия целевой патологии превышает вероятность его отсутствия [2]. Насколько более вероятно то, что тест будет положительным у человека с заболеванием по сравнению со здоровым? [3]

Метрика используется для интерпретации диагностических тестов. Отношение правдоподобия для положительных результатов теста (LR+) равняется вероятности положительного результата теста для человека с заболеванием, деленное на вероятность положительного результата теста для человека без заболевания.

7. Отношение правдоподобия отрицательного результата (Likelihood ratio for negative results / LR-)

Формула:     (1-чувствительность)/ специфичность

Описание: Отображает, во сколько раз при отрицательном результате СИИ вероятность наличия целевой патологии превышает вероятность его отсутствия [2].

Метрика используется для интерпретации диагностических тестов.  Это вероятность отрицательного результата теста для больного человека, деленная на вероятность отрицательного результата теста для здорового человека.

Интерпретация LR+ и LR-:

Отношения правдоподобия (LR) являются альтернативой прогностическим ценностям положительных и отрицательных результатов для оценки вероятности заболевания после диагностического тестирования. Общая формула отношения правдоподобия - это вероятность (P) того, что у человека с заболеванием будет определенный результат теста, деленная на вероятность того, что у человека без заболевания будет тот же результат:

LR = P(результат теста с заболеванием) / P(результат теста без заболевания).

Существует два типа отношений правдоподобия: положительное и отрицательное:

Отношение правдоподобия положительного результата (LR+) - это вероятность того, что у человека с заболеванием будет положительный результат теста, деленная на вероятность того, что у человека без заболевания будет положительный результат.

Отношение правдоподобия отрицательного результата (LR-) - это вероятность того, что у человека с заболеванием будет отрицательный результат теста, деленная на вероятность того, что у человека без заболевания будет отрицательный результат. Чем выше LR+, тем больше вероятность того, что у человека, сдавшего положительный анализ, есть данное заболевание. Чем ниже LR-, тем больше вероятность того, что у человека с отрицательным тестом нет данного заболевания. LR+ или LR-, равные единице, означают, что вероятность положительного или отрицательного теста у людей с заболеванием и без него одинакова, т.е. тест не может отличить тех, у кого есть заболевание, от тех, у кого его нет. Как правило, LR+ больше 10 и LR- меньше 0,1 говорят о том, что тест надежно различает людей, у которых есть и у которых нет заболевания [5].

Эвристический подход к определению значений LR [6]:

• Значения LR+ больше 10 или LR- менее 0,1, являются очень эффективными и убедительными;
• Значения LR+, варьирующие от 5 до 10, или LR- от 0,1 до 0,2, оказывают умеренное влияние на вероятность;
• Значения LR+ в диапазоне от 2 до 5 или LR- от 0,2 до 0,5 оказывают незначительное влияние на вероятность;
• Значения LR в диапазоне от 0,5 до 2 мало убедительны

Зависимость вероятности заболевания от коэффициента правдоподобия [7]

Отношение правдоподобия    Приблизительное изменение вероятности (%)

Значения от 0 до 1 снижают вероятность заболевания (LR-) 

Значения, превышающие 1, увеличивают вероятность заболевания (LR+)    

 8. Коэффициент детерминации (R2 score)

Формула: 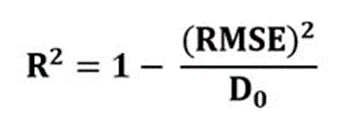     , где D0 это дисперсия реальных значений.

Описание: Является показателем для оценки адекватности модели машинного обучения на основе линейной регрессии для прогнозирования выбранного показателя [8]

Интерпретация:

Коэффициент детерминации R2 может принимать значения от 0 до 1. Если R2 <0, то метод прогнозирования является неадекватным на выбранных данных. То есть реальные значения показателя находятся ближе к своему среднему значению, чем к прогнозам. Если R2 = 0, то метод прогнозирования ничем не лучше прогноза средним значением показателя (прогноза нулевого уровня). Если 0 <R2 <1, то метод прогнозирования является адекватным для выбранных данных. То есть прогнозы лежат к реальным значениям показателя ближе, чем реальные значения к их среднему значению [9]. Предполагается, что чем выше значение R2, тем лучше модель описывает данные, однако низкие значения R2 не всегда означают, что модель плоха и, наоборот, высокие значения R2 не всегда говорят о том, что модель хороша [10].  Таким образом, коэффициент детерминации нужен только для того, чтобы увидеть, что он положительный, и тем самым убедиться, что мы имеем дело с адекватными прогнозами модели.

9. Оценка Брайера (Brier score)

Формула: 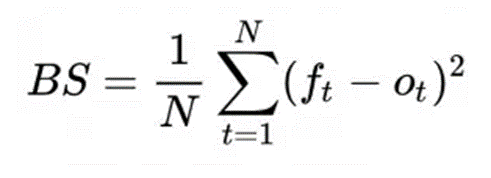     ,где:

f = прогнозируемая вероятность
o = результат (1, если событие произошло, 0, если оно не произошло)

Описание: Используется в статистике для измерения точности вероятностных прогнозов. Обычно он используется, когда результат прогноза является бинарным — целевое событие либо происходит, либо не происходит [8].

Интерпретация:

Оценка Брайера может принимать любое значение от 0 до 1, где 0 — это наилучшая достижимая оценка, а 1 — наихудшая достижимая оценка. Чем ниже оценка Брайера, тем точнее прогноз. На практике оценка Брайера, равная 0.25, может означать, что прогноз лишь незначительно лучше, чем случайное угадывание, тогда как оценка, близкая к 0, указывает на высокий уровень точности прогнозирования.

II. Показатели дискриминации (Discrimination)

Показатели дискриминации используются в задачах бинарной классификации для определения того, насколько хорошо модель разделяет пациентов на классы.

10. F1-мера (F1-Score)

Формула:     2 * ПЦПР * чувствительность / (ПЦПР + чувствительность)

Описание: Среднее гармоническое между ПЦПР и чувствительностью.

Интерпретация:

Оценки F1 могут варьироваться от 0 до 1, где 1 представляет модель, которая идеально классифицирует каждое наблюдение в правильный класс, а 0 представляет модель, которая не может классифицировать какое-либо наблюдение в правильный класс.
Не существует конкретного значения, которое считается «хорошим» результатом F1, поэтому обычно выбирается модель классификации, которая дает наивысший балл F1.
 
11. Рабочая характеристика приемника или ROC-кривая (ROC / Receiver operating characteristic)

Формула:     TPR = ИП/ИП+ЛО
                      FPR = ЛО/ЛО+ИО

ROC-кривая - график, где TPR расположена по оси Y и FPR расположена по оси X

Описание: График, показывающий зависимость верно классифицируемых объектов положительного класса от ложно положительно классифицируемых объектов негативного класса. Иными словами, соотношение True Positive Rate (Recall) и False Positive Rate.

Интерпретация:
 
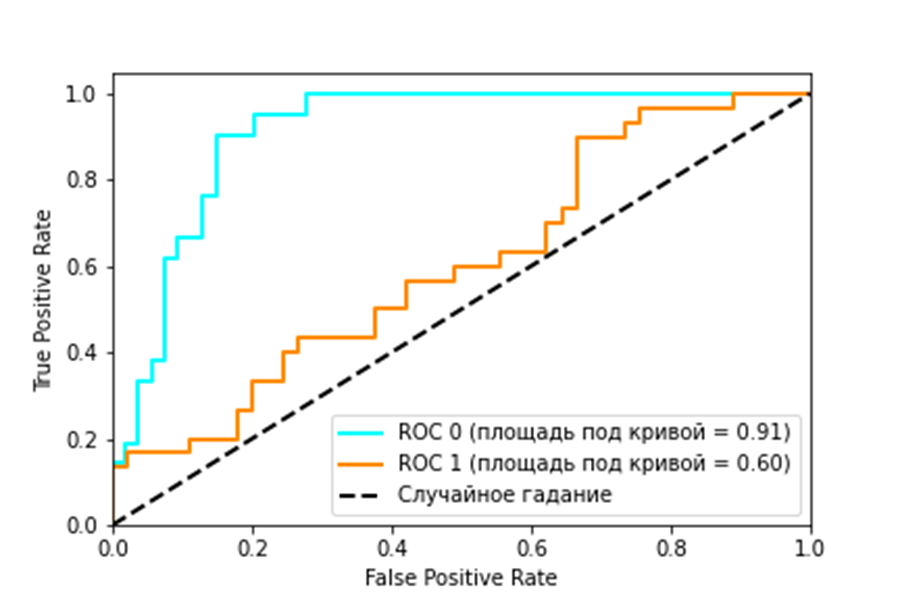
Рисунок 1: ROC кривая

Рисунок 1 содержит пример двух ROC – кривых. Идеальное значение графика находится в верхней левой точке (TPR = 1, a FPR = 0). При этом, кривая, соответствующая FPR = TPR является случайным гаданием. Говорят, что кривая X доминирует над другой кривой Y, если X в любом точке находится левее и выше Y [11], что означает превосходство первого классификатора над вторым.

С помощью ROC — кривой, можно сравнить модели, а также их параметры для поиска наиболее оптимального соотношения TPR и FPR. В этом случае ищется компромисс между количеством пациентов, класс которых был правильно определен как положительный и количеством пациентов, класс которых был некорректно определен как положительный.

12. Площадь под ROC кривой (AUC / Area Under Curve)

Формула: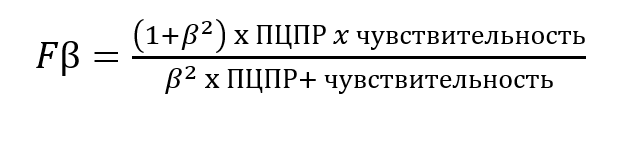

Описание: Численная оценка ROC кривой (площадь под этой кривой).

Интерпретация:

Все предыдущие метрики позволяют оценить качество модели только при определённом пороге классификации. AUC позволяет оценить дифференцирующее качество модели без зависимости от порога.

В идеальном случае ROC-кривая будет стремиться в верхний левый угол (TPR=1 и FPR=0), а площадь под ней (AUC) будет равна единице. При значении площади 0.5 качество прогнозов модели будет сопоставимо случайному угадыванию, ну а если это значение меньше 0.5, то, модель лучше предсказывает результаты, противоположные истинным — в таком случае нужно просто поменять целевые классы местами для получения площади больше 0.5 [12].

ROC-AUC не очень хорошо справляется с сильным дисбалансом классов, поскольку учитывает истинно отрицательные случаи (ИО), что вытекает из расчётов FPR. Проще говоря, модель может показать высокий TPR, но при этом также иметь большое количество ложноположительных предсказаний (FPR).

13. Площадь под Precision - Recall кривой (PR-AUC)

Формула:     Precision = ИП/(ИП + ЛП)
                     Recall = ИП/(ИП + ЛО)

PR кривая - график, где Precision расположена по оси Y и Recall расположена по оси X

Описание: Численная оценка Precision - Recall кривой (площадь под этой кривой).

Интерпретация:

PR-AUC лучше подходит для данных с сильным дисбалансом классов. Это связано с тем, что PR-AUC фокусируется на соотношении истинно положительных и ложноотрицательных результатов, что лучше отражает способность модели правильно определять положительные классы и, следовательно, лучше справляться в задачах ранжирования, где это необходимо в первую очередь. Например, если мы хотим показать пользователю наиболее релевантные фильмы, PR-AUC будет лучше учитывать действительно интересные для пользователя фильмы (ИП), в то время как ROC-AUC может учесть наименее интересные фильмы (ИО). Также стоит добавить, что в отличие от ROC-AUC, на графике PR-AUC будет стремиться в правый верхний угол.

Однако и здесь не всё так просто, поскольку интерполяцию между двумя точками в ROC-пространстве можно выполнить, просто соединив их прямой линией, то в PR-пространстве интерполяция может иметь более сложную связь. При изменении уровня Recall, метрика Precision не обязательно будет изменяться линейно, поскольку ЛП заменяет ЛО в знаменателе Precision. В таком случае линейная интерполяция является ошибочной и может давать слишком оптимистичную оценку качества модели. Проще говоря, в случае PR-AUC такой подход может считать завышенную площадь под кривой [12].

14. Средняя ПЦПР (скорректированная) (Average Precision score (adjusted))

Формула:     

Описание: Это масштабированная площадь под кривой PR, которая представляет собой площадь под всеми определенными точками кривой PR, умноженную на масштабный коэффициент, корректирующий «недостающую площадь» под неопределенными точками, если таковые имеются. Если кривая полностью определена, то AP (скорректированный) идентичен PR-AUC.

Интерпретация:

Как и AUC ROC, AUC PR - это площадь под кривой PR. Однако в некоторых ситуациях при достаточно высоких пороговых значениях ПЦПР может быть не определена (При достаточно высоком пороге может не быть ни одного истинно положительного результата (ИП = 0), но также, поскольку порог слишком высок, может не быть и ни одного ложноположительного результата (ЛП = 0). Это приводит к значению Precision = 0 / 0, которое не определено), и под неопределенными значениями ПЦПР нет «области». Поэтому для сравнения площади под кривой между моделями, имеющими полную кривую, и моделями, не имеющими ее, определяется средний балл ПЦПР (скорректированный).
Средняя оценка ПЦПР (скорректированная) является наилучшим показателем в случае, когда положительный класс составляет меньшинство [13].

15. Сбалансированная точность (Balanced accuracy)

Формула:     Balanced accuracy = (Чувствительность + Специфичность) / 2

Описание: Среднее чувствительности (Sensitivity) и специфичности (Specificity).

Интерпретация:

В отличие от традиционной точности, которая может вводить в заблуждение в несбалансированных наборах данных, сбалансированная точность обеспечивает более детальную картину, принимая во внимание истинно положительный уровень (чувствительность) и истинно отрицательный уровень (специфичность). Этот показатель особенно ценен в сценариях, где классы представлены неравномерно, например, при медицинской диагностике. В медицинской диагностике это помогает оценить эффективность моделей, прогнозирующих заболевания, гарантируя учет как ложноотрицательных результатов (пропущенный диагноз), так и ложноположительных результатов (ненужное лечение).

Интерпретация сбалансированных показателей точности требует понимания контекста, в котором применяется модель. Сбалансированная оценка точности 0.5 указывает на то, что модель работает не лучше, чем случайное угадывание, а оценка 1.0 означает идеальную классификацию. Результаты между этими крайностями могут дать представление о сильных и слабых сторонах модели. Например, сбалансированная оценка точности 0.7 может свидетельствовать о том, что модель достаточно эффективна, но может потребоваться дальнейшее исследование прогнозов конкретного класса для выявления областей для улучшения [14].

16. G-среднее (G mean)

Формула:     G=√(чувствительность x специфичность)

Описание: Геометрическое среднее между чувствительностью и специфичностью.

Интерпретация:

G-среднее - одна из наиболее часто используемых метрик при работе с несбалансированными наборами данных [15].

Возможный диапазон значений от 0 до 1. Наилучшая возможная оценка – 1 (чем большее значение, тем лучше).

Для задач бинарной классификации с двумя классами показатель G-среднее представляет собой одно значение, отражающее общую точность модели. Показатель G-среднее, равный 1, означает идеальную точность, в то время как показатель менее 1 указывает на то, что один из классов определяется ошибочно чаще, чем другой.

В задаче мультиклассификации показатель G-среднее может быть рассчитан для каждого класса, а затем усреднен по всем классам, чтобы получить единое значение, отражающее общую точность модели. Среднее значение может быть взвешенным или невзвешенным, в зависимости от желаемой интерпретации результатов.

Показатель G-среднего дает возможность сбалансировать точность модели между положительными и отрицательными классами и особенно полезен в случаях, когда распределение классов несбалансировано или когда один класс важнее другого [16].

17. F_бета мера (Fβ score)

Формула:     Fβ=((1+β^2 )  x ПЦПР x чувствительность)/(β^2  x ПЦПР+ чувствительность)

где β представляет собой константу для корректировки относительной важности чувствительности по отношению к ПЦПР.
Описание: F_бета мера является более общей формой F1-меры. Это взвешенное среднее гармоническое значение для ПЦПР и чувствительности.
Интерпретация:
F_бета мера используется при работе с несбалансированными наборами данных. Она более информативна, чем F1-мера, в отношении эффективности классификатора по правильному предсказанию случаев в меньшем классе [15].

Что делать, если чувствительность и ПЦПР не одинаково важны? Бывают случаи, когда один из показателей важнее другого.

Мы больше заботимся о чувствительности, если ложноотрицательный результат является более серьезной ошибкой, чем ложноположительный. В качестве примера можно привести диагностические ML-инструменты в медицине. Там ложноотрицательный результат - это пропущенное заболевание, которое может оказаться фатальным для здоровья пациента.

И наоборот, ПЦПР важнее, когда ложноположительный результат имеет большую цену. Так обстоит дело с обнаружением спама. Если позволить спаму появляться в папке входящих сообщений, это может раздражать пользователя, но, если пометить не спамное письмо как спам и отправить его в мусорную корзину, это может привести к потере возможности трудоустройства.

В таких ситуациях мы бы хотели иметь метрику, учитывающую относительную важность чувствительности и ПЦПР. F_бета мера является именно такой метрикой. Если β >1, то чувствительность в β раз важнее ПЦПР. Если β <1, то все наоборот [17].

III. Показатели клинической полезности (Clinical usefulness)

18. Чистая выгода (Net benefit)

Формула:     Net benefit = ИП/N – ЛП/N * Pt/(1-Pt),
                     где Pt – пороговая вероятность,
                     N – объем выборки
или
выгода-(вред × курс обмена)

Описание: Чистая выгода - это простой вид анализа решений, при котором выгода и вред помещаются на одну шкалу, чтобы их можно было сравнивать напрямую.

Интерпретация:

Чистая выгода похожа на идею чистой прибыли в бизнесе. Возьмем импортера, который закупает вино во Франции на 1 млн евро и продает его в США за 1,5 млн долларов. Чтобы рассчитать прибыль, доллары и евро должны находиться в одной шкале, используя обменный курс. Если 1 евро стоит 1,25 доллара, то прибыль = доход в долларах (1,5 млн)-расход в евро (1 млн) ×1,25=250000 долларов. Чистая выгода применяет аналогичную методологию к медицинским исследованиям, определяя обменный курс между различными медицинскими конечными точками, такими как обнаружение рака по сравнению с ненужной биопсией.

Представим концепцию чистой выгоды в медицинских исследованиях на примере биопсии при раке простаты. Мужчины с повышенным уровнем простатоспецифического антигена (ПСА) подвержены повышенному риску рака простаты и часто направляются на биопсию простаты. Но у большинства мужчин с высоким уровнем ПСА либо нет рака, либо есть только доброкачественные опухоли, которые не нуждаются в лечении.

Биопсия не только инвазивна и неприятна, но и может стать причиной инфекции. Исследователи активно ищут дополнительные маркеры, которые можно было бы использовать в качестве теста у мужчин с повышенным уровнем ПСА, чтобы уточнить показания к биопсии.

Представьте, что мы хотим проанализировать исследование нового маркера рака простаты. В исследование вошли 100 мужчин, у всех из которых был повышен уровень ПСА без очевидной причины, и поэтому они были кандидатами на биопсию. Мы предположим, что результаты будут такими: рак у 25 пациентов; когда были проанализированы образцы крови всех 100 пациентов, у 72 был обнаружен высокий уровень нового маркера, из которых у 22 был рак.

Чтобы проанализировать исследование с помощью метода чистой выгоды, нам нужно определить обменный курс, учитывая количество мужчин, которым врач сделал бы биопсию, чтобы найти одного с раком простаты. Разумным ответом будет то, что для обнаружения одного мужчины с раком биопсию следует проводить не более чем у 10 мужчин. Это означает, что вред от отсрочки диагностики рака в девять раз больше, чем вред от ненужной биопсии (у 10 мужчин, подвергшихся биопсии, обнаруживается один рак, а на каждый обнаруженный рак приходится девять ненужных биопсий). Поэтому в нашем анализе мы хотим «взвесить» обнаружение рака высокой степени как в девять раз более важное, чем избежание ненужной биопсии. Используя принцип, аналогичный расчету прибыли при импорте вина, мы можем использовать 1÷9 в качестве обменного курса. Мы определяем чистую выгоду как: выгода-(вред × курс обмена). Чистая выгода от проведения биопсии у всех мужчин составляет 25%-(75%×(1÷9))=16,7%; чистая выгода, если бы новый маркер использовался для определения биопсии, составляет 22%-(50%×(1÷9))=16,4%. Поскольку при данном конкретном обменном курсе чистая выгода для маркера ниже, чем для биопсии у всех мужчин, можно сделать вывод, что использование маркера для определения биопсии приведет к худшему клиническому результату, чем текущая практика биопсии у всех мужчин с повышенным уровнем ПСА, не обусловленным доброкачественным заболеванием.

Единицей измерения чистой выгоды являются истинные положительные результаты. Таким образом, чистая выгода в 16,4% означает, что маркер эквивалентен стратегии, которая привела бы к биопсии у 164 мужчин на 1000 человек из группы риска, при этом все результаты биопсии были бы положительными в отношении рака. Это сопоставимо с понятием прибыли. Если оставить в стороне проблему финансового риска, то прибыль в 250 000 долларов при сделке с вином примерно эквивалентна тому, что вы просто получили 250000 долларов, не тратя деньги на покупку вина.

Еще одно сходство между прибылью и чистой выгодой заключается в том, что порядок ранжирования более важен, чем размер разницы. Виноторговец, вынужденный выбирать между двумя конкурирующими сделками, выберет более выгодную, практически независимо от того, будет ли прибыль выше на $1000 или на $100 000.
Точно так же мы обычно выбираем стратегию с наибольшей чистой выгодой, не заботясь о размере разницы в чистой выгоде.

Одно из очевидных критических замечаний в адрес чистой выгоды в медицине заключается в том, что обменный курс - это субъективная переменная. Можно легко варьировать обменный курс и посмотреть, как это влияет на результаты. Например, если врач готов провести 20 биопсий, чтобы найти одного пациента с раком, чистая выгода от биопсии у всех мужчин (то есть 25%-(75%×(1÷19))=21,1%) все равно выше, чем от использования маркера (то есть 22%-(50%×(1÷19))=19,4%) [18].

19. Кривая принятия решений (Decision curve)

Формула:     График, где на оси X - диапазон порогов срабатывания, на оси Y – значение чистой выгоды.

Описание: График чистой выгоды для широкого диапазона обменных курсов (порогов срабатывания, порогов принятия решений, дискриминационных порогов).

Чтобы увидеть, как меняется чистая выгода при различных порогах срабатывания, мы используем алгоритм:

1. Выбираем порог (Pt), чтобы определить, когда пациент является положительным.
2. Подсчитываем количество пациентов с положительным результатом (риск ≥ Pt), у которых есть заболевание (истинно положительные результаты), по сравнению с теми, у кого результат положительный, но нет заболевания (ложноположительные результаты).
3. Рассчитываем чистую выгоду при N - общем объеме выборки.
4. Повторяем шаги 2 и 3 для разумного диапазона порогов срабатывания.
5. Повторяем все шаги для каждого маркера, модели или теста в исследовании, а также для стратегий «по умолчанию» - лечить всех мужчин или не лечить никого, если результат положительный.

Интерпретация:

 
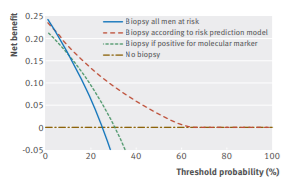
Рисунок 2: Кривая принятия решений

График на рисунке 2 показывает чистую выгоду маркера и статистической модели, а также двух клинических альтернатив - проведения биопсии у всех мужчин или ни у кого из них.

Основная интерпретация кривой принятия решений заключается в том, что стратегия с наибольшей чистой выгодой при определенном пороге срабатывания имеет наибольшую клиническую ценность. Мы отмечаем, что чистая выгода для маркера ниже, чем для стратегии «биопсия у всех» при пороге срабатывания ниже 11%. Для несклонных к риску врачей или пациентов с низким порогом, скажем, 5%, это означает, что наилучший клинический результат - количество ненужных биопсий и выявленных раков - будет достигнут при проведении биопсии независимо от результатов маркера. При пороговом значении, скажем, 20%, чистая выгода от использования маркера выше, чем от проведения биопсии у всех, поэтому оптимальной клинической стратегией будет проведение биопсии только у тех мужчин, у которых маркер положителен. Ключевым моментом является то, что маркер полезен только для подгруппы предпочтений [18].

IV. Многоклассовая классификация (Multiclass classification)

Формула:   

Описание: Мульти-классификация - это способность модели классифицировать входные данные на более чем два класса. Одним из возможных способов является вычисление среднего метрики по всем классам, где в качестве «положительного» класса берется вычисляемый, а все остальные — в качестве «отрицательного» [19].

Интерпретация:

Все рассмотренные выше метрики относились лишь к бинарной задаче, но, зачастую, классов больше, чем два. Это обуславливает необходимость в обобщении рассмотренных метрик. Одним из возможных способов является вычисление среднего метрики по всем классам.

Существует два подхода: попарное сравнение либо один против всех.

Стратегия «один против всех» является наиболее часто используемой и заключается в создании бинарных классификаторов для каждого класса. Например, если у нас есть 3 класса (A, B, C), то мы создаем три классификатора: один для класса A против (B+C), второй для класса B против (A+C) и третий для класса C против (A+B). Затем, чтобы сделать прогноз для новых данных, каждый классификатор предсказывает вероятность принадлежности объекта к своему классу, и выбирается класс с наибольшей вероятностью. Помимо вычислительной эффективности, одним из преимуществ этого подхода является его интерпретируемость.

При «попарном сравнении» создается отдельный классификатор для каждой пары классов. Во время прогнозирования выбирается класс, набравший наибольшее количество голосов. Этот метод обычно работает медленнее, чем «один против всех», из-за его сложности [20].

Стоит отдельно выделить метрику Average Precision, которая является альтернативной (и очень схожей) метрикой для PR-AUC. Её основное отличие как раз и заключается в том, что для расчёта не используется линейная интерполяция. Вместо этого кривая Precision-Recall суммируется как средневзвешенное значение Precisions, полученное для каждого порога, а в качестве веса используется увеличение Recall по сравнению с предыдущим порогом.

Представленный перечень метрик оценки моделей прогнозирования и диагностики включает в себя наиболее распространенные метрики для моделей, работающих с табличными данными. Для моделей, анализирующих медицинские изображения и сигналы, существуют отдельные метрики, характеризующие точность локализации целевых патологий наравне с общей точность классификации. Так как каждая из метрик характеризует разные аспекты производительности моделей, не существует единой метрики для всесторонней и объективной оценки. Поэтому целевые метрики должны определятся исходя из клинико-практической задачи, которую планируется решать с помощью моделей, а также состава набора данных, на котором модель обучалась и тестировалась. Кроме для большинства метрик должны быть приведены доверительные интервалы 95% или 99% для оценки ожидаемого разброса ее значений.

Источники.

1.     Morozov, Sergey, Vladzymyrskyy, Anton, Кляшторный, Владислав, Andreychenko, Anna, Kulberg, Nicholas, Gombolevskiy, Victor. (2019). Клинические испытания программного обеспечения на основе интеллектуальных технологий (лучевая диагностика). Препринт № ЦДТ-2019-1
2.     ГОСТ Р 59921.1—2022
3.     Гринхальх, Т. Основы доказательной медицины / Т. Гринхальх ; пер. с англ. под ред. В. В. Власова. - 5-е изд. , перераб. и доп. - Москва : ГЭОТАР-Медиа, 2022. - 328 с. - ISBN 978-5-9704-5832-7.   
4.     https://www.googlawi.com/ru/blog/health/a-z/sexually-transmitted-diseases-stds/Negative-Predictive-Value-of-a-Test/
5.     https://radiopaedia.org/articles/likelihood-ratios?lang=us
6.     Fischer BG, Evans AT. SpPin and SnNout Are Not Enough. It's Time to Fully Embrace Likelihood Ratios and Probabilistic Reasoning to Achieve Diagnostic Excellence. J Gen Intern Med. 2023 Jul;38(9):2202-2204. doi: 10.1007/s11606-023-08177-5. Epub 2023 Apr 3. PMID: 37010678; PMCID: PMC10361927.
7.     McGee S. Simplifying likelihood ratios. J Gen Intern Med. 2002 Aug;17(8):646-9. doi: 10.1046/j.1525-1497.2002.10750.x. PMID: 12213147; PMCID: PMC1495095.
8.     Steyerberg EW, Vickers AJ, Cook NR, Gerds T, Gonen M, Obuchowski N, Pencina MJ, Kattan MW. Assessing the performance of prediction models: a framework for traditional and novel measures. Epidemiology. 2010 Jan;21(1):128-38. doi: 10.1097/EDE.0b013e3181c30fb2. PMID: 20010215; PMCID: PMC3575184.
9.     https://forecast.nanoquant.ru/metric/r2.htm
10.     https://statisticsbyjim.com/regression/interpret-r-squared-regression/
11.     https://www.researchgate.net/publication/3297379_Using_AUC_and_Accuracy_in_Evaluating_Learning_Algorithms
12.     https://habr.com/ru/articles/821547/
13.     https://www.pi.exchange/knowledgehub/metrics-to-consider-when-evaluating-a-binary-classification-models-performance
14.     https://ru.statisticseasily.com/глоссарий/what-is-balanced-accuracy/
15.     Albuquerque J, Medeiros AM, Alves AC, Bourbon M, Antunes M. Comparative study on the performance of different classification algorithms, combined with pre- and post-processing techniques to handle imbalanced data, in the diagnosis of adult patients with familial hypercholesterolemia. PLoS One. 2022 Jun 24;17(6):e0269713. doi: 10.1371/journal.pone.0269713. PMID: 35749402; PMCID: PMC9231719.
16.     https://permetrics.readthedocs.io/en/v2.0.0/pages/classification/GMS.html
17.     https://www.baeldung.com/cs/f-beta-score
18.     Vickers AJ, Van Calster B, Steyerberg EW. Net benefit approaches to the evaluation of prediction models, molecular markers, and diagnostic tests. BMJ. 2016 Jan 25;352:i6. doi: 10.1136/bmj.i6. PMID: 26810254; PMCID: PMC4724785.
19.     https://www.researchgate.net/publication/286914533_On_extending_f-measure_and_g-mean_metrics_to_multi-class_problems
20.     https://scikit-learn.org/stable/modules/multiclass.html#multiclass-classification