
Пропуски в значениях данных – частая сложность при разработке моделей машинного обучения. Для случаев со случайными пропусками значений параметров существует целый ряд методов и подходов. Однако по мере того, как исследования в области машинного обучения становятся все более глобальными и стремятся к получению знаний из все больших объемов разнородных данных и источников, все чаще возникает ситуация, в которой отсутствующие значения явно или неявно демонстрируют взаимосвязи или структуру. Такие системные либо структурированные пропуски представляют собой фундаментальное препятствие для масштабного машинного обучения.
Текст данного блога составлен на основе недавней статьи в журнале Nature, описывающей существующие сложности и подходы машинного обучения на данных со системными/структурированными пропусками.
Обращение с недостающими данными является давно известной сложностью в статистике и машинном обучении (ML) (Little, R. J. A. & Rubin, D. B. Statistical Analysis With Missing Data Vol. 793 (John Wiley & Sons, 2019); Karlaš, B. et al. Nearest neighbor classifiers over incomplete information: from certain answers to certain predictions. Preprint at https://arxiv.org/abs/2005.05117 (2020)).
Существует широкий спектр способов обработки случайно отсутствующих данных (Rubin, D. B. Inference and missing data. Biometrika 63, 581–592 (1976)), основанных на хорошо разработанной теории. Однако во многих задачах значения данных могут отсутствовать не случайно, а проявлять системность или закономерность (Emmanuel, T. et al. A survey on missing data in machine learning. J. Big Data 8, 1–37 (2021).
Эти проблемы особенно актуальны в областях, требующих объединения данных, многовариантного обучения и/или связывания данных, содержащих информацию из нескольких источников и исследований. Для развития в этих областях, необходимо решить задачи обращения с такими данными и обучения моделей на данных с высокой "структурированностью пропусков" (Structured Missingness, SM).
Структурированные/системные пропуски могут возникать по многим причинам.
В блоке 1 представлены некоторые варианты появления SM, отражающие разнообразие способов, которыми SM может естественным образом возникать в современных исследованиях и машинном обучении. Возможно, что наиболее актуально для масштабного ML, SM естественно возникает при объединении мультимодальных наборов данных или, когда данные описывают свойства неоднородной группы людей с различными характеристиками.
Например, в контексте здравоохранения и медицины SM возникает при объединении исторических клинических, геномных данных и данных медицинской визуализации (Topol, E. J. High-performance medicine: the convergence of human and artificial intelligence. Nat. Med. 25, 44–56 (2019)) или при решении задач с широким охватом, таких как разработка моделей прогнозирования, включающих диагностические измерения для различных видов раковых заболеваний, которые, следовательно, имеются только у подмножества пациентов (Silva, L. A. V. & Rohr, K. Pan-cancer prognosis prediction using multimodal deep learning. In 2020 IEEE 17th International Symposium on Biomedical Imaging 568–571 (IEEE, 2020)).
В более широком смысле, SM обычно возникает при объединении информации из нескольких исследований, каждое из которых может отличаться по дизайну и набору параметров и, следовательно, содержать только подмножество параметров из объединённых методов измерения. В таких ситуациях отсутствующие значения могут быть связаны с различными методологиями, использованными для сбора данных, или отражать характеристики более широкой популяции (что может представлять определенный интерес).
Поэтому системность и закономерности пропусков могут нести ценную информацию при разработке моделей машинного обучения. Несмотря на такую потенциальную ценность, наличие SM обычно существенно ограничивает способность эффективно использовать данные для моделирования и может серьезно затруднить процесс анализа, в том числе построение логических моделей, разработку алгоритмов прогнозирования и классификации, а также создание информативных визуальных представлений данных. Обзор различных проблем, связанных с жизненным циклом пропущенных данных, приведен на рис. 1.
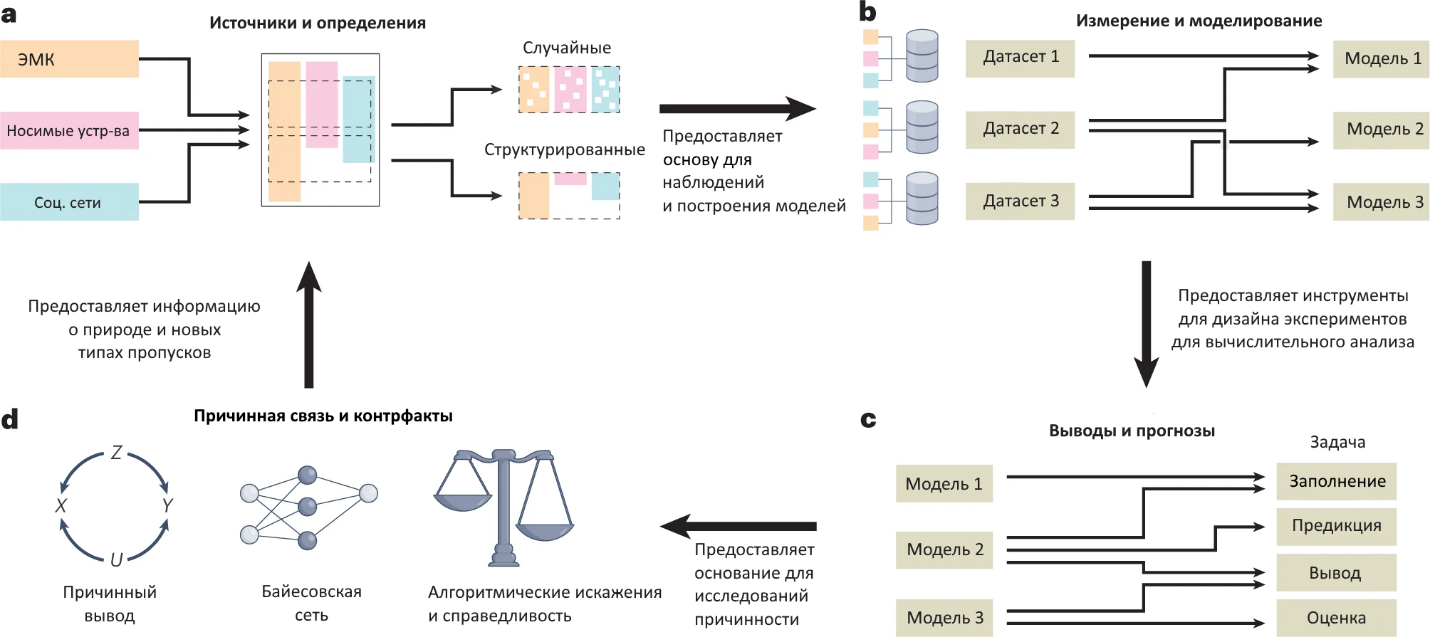
Рис. 1: Жизненный цикл пропущенных данных.
Наличие SM влияет на все аспекты жизненного цикла сбора и анализа данных.
- Данные могут быть собраны из множества различных источников - в данном примере из электронных медицинских карт, носимых устройств и социальных сетей. При объединении этих данных могут возникать как случайные, так и структурированные/системные пропуски. Понимание взаимосвязи и отличий между случайным пропуском в данных и SM требует новой теории и инструментов, включая новые инструменты проектирования для минимизации влияния SM на последующий анализ. Задачи 1-3 связаны с этими вопросами.
- SM влияет на наши подходы к моделированию, которые обеспечивают надлежащее и непредвзятое обучение. Необходимы новые инструменты для надлежащей обработки SM и новые архитектуры и методы, адаптирующиеся к SM в контексте прогнозирования или выводов. Задачи 4 и 5 связаны с этими проблемами.
- Эффективность модели часто (хотя и не всегда) зависит от способности корректно заполнять отсутствующие значения в данных. Поэтому необходимы новые инструменты для обращения и заполнения SM, а также инструменты для сравнения и оценки эффективности методов, моделирующих и работающих с SM, включая задачи прогнозирования, классификации и логических выводов. С этими вопросами связаны задачи 4-7.
- Во многих научных контекстах конечной целью любого обучения является развитие лучшего понимания причинности, например, вывод причинно-следственных связей между переменными U, X, Y, Z. Наличие SM может негативно сказаться на этих выводах. Необходимы более совершенные инструменты для количественной оценки и определения причинно-следственных связей из данных с SM, а также методы оценки того, в какой степени отсутствующие данные связаны с системными погрешностями и техническими сбоями в процессах сбора данных, что, в свою очередь, может затруднить вывод причинно-следственных механизмов и привести к необъективным или несправедливым результатам моделирования. Задачи 8 и 9 связаны с этими проблемами. Решение проблем на каждом этапе жизненного цикла отсутствующих данных имеет ключевое значение для обеспечения надлежащего анализа и формирования представлений на основе данных с SM.
Существующие методы работы с отсутствующими данными, такие как (множественное) заполнение (imputation) (Rubin, D. B. Multiple imputation after 18+ years. J. Am. Stat. Assoc. 91, 473–489 (1996)), обычно не учитывают структуру отсутствующих данных и поэтому могут не справиться с SM должным образом.
По мере продвижения к разработке моделей ML, которые могут обучаться на многоцентровых массивах данных и выполнять многочисленные последующие задачи (такие как фундаментальные модели) и/или использовать объединительные («федеративные», federated) подходы к обучению, эти вопросы становятся все более актуальными.
Действительно, проблемы отсутствия данных являются основным препятствием для эффективного масштабируемого обучения (Holmes, C. Artificial Intelligence and Health: A Summary Report of a Roundtable Held on 16 January 2019 (Academy of Medical Sciences, 2019); https://acmedsci.ac.uk/policy/policy-projects/artificial--intelligence-and-health). Однако, несмотря на распространенность этой проблемы, SM еще не изучена систематически, и нам не хватает как теории SM, так и инструментов, необходимых для эффективного обучения на данных с SM.
Если инструменты и существуют, то они рассеяны по различным дисциплинам и сфокусированы в первую очередь на адаптации существующих методов машинного обучения для решения конкретных проблем SM. Например, в статье Dong, X. et al. TOBMI: trans-omics block missing data imputation using a k-nearest neighbor weighted approach. Bioinformatics 35, 1278–1283 (2019) рассматриваются адаптации методов k-ближайших соседе для заполнения блочных недостающих данных, возникающих при объединении данных из нескольких высокопроизводительных масштабных экспериментов «омики» (omics).
В аналогичном биомедицинском контексте в статье Naito, T. et al. A deep learning method for HLA imputation and trans-ethnic MHC fine-mapping of type 1 diabetes. Nat. Commun. 12, 1639 (2021) использовались инструменты многозадачного обучения для заполнения блоков отсутствующих генотипов. С более теоретической точки зрения, в статье Audigier, V. et al. Multiple imputation for multilevel data with continuous and binary variables. Stat. Sci. 33, 160–183 (2018) рассматривается адаптация многоуровневой модели для многократного заполнения отсутствующих значений, когда они возникают систематически. Кроме того, в работе Kamphuis, R., Jolani, S. & Lugtig, P. The blocked imputation approach for missing data. Preprint at ResearchGate https://doi.org/10.13140/RG.2.2.12467.32803 (2018) предложен способ заполнения блочных отсутствующих значений, который расширяет классическую методологию множественного заполнения пропусков.
В целом, исследователи начинают обращать внимание на возможности методов ML, таких как древовидные инструменты и глубокое обучение, для заполнения отсутствующих значений и/или понимания структуры пропущенных значений, хотя релевантная литература все еще находится в зачаточном состоянии Che, Z., Purushotham, S., Cho, K., Sontag, D. & Liu, Y. Recurrent neural networks for multivariate time series with missing values. Sci. Rep. 8, 6085 (2018). Таким образом, хотя исследования и рассматривали проблемы SM в конкретных условиях, предложенные методы, как правило, являются частными решениями с ограниченной применимостью.
Блок 1: Источники SM
Системные/Структурированные пропуски - это широкий термин, относящийся к неслучайным многомерным моделям пропусков в наборе данных. Они могут возникать разными способами, каждый из которых имеет свои особенности и проблемы. Тем не менее, существуют некоторые общие процессы, которые приводят к возникновению SM в контекстах ML. Здесь мы описываем пять из них.
Мультимодальная связь
Структурированная пропущенная информация естественным образом возникает всякий раз, когда данные, полученные из разных источников, процессов или экспериментов, связываются вместе. Такая связь данных становится все более распространенной, и связанные данные используются для обучения некоторых из самых мощных современных ML-моделей. В этом случае каждый блок данных может быть получен только с помощью подмножества доступных способов измерения. Во блоке 2 приведен наглядный пример проблем, возникающих при использовании такого рода SM в большом наборе биомедицинских данных Singal, G. et al. Development and validation of a real-world clinicogenomic database. J. Clin. Oncol. 35, 2514 (2017).
Связь данных различных масштабов
Системный пропуск естественно возникает всякий раз, когда объединяются измерения в различных пространственных или временных масштабах. Например, при геопространственном анализе различные датчики могут измерять различные аспекты климата. Некоторые из этих измерений (например, температура поверхности моря, которую можно относительно легко получить со спутниковых инфракрасных датчиков) могут быть подробно измерены в пространстве и времени, тогда как другие (например, осадки) получить сложнее, и они могут быть измерены с низкой недостаточной частотой. При совместном рассмотрении получаемые данные имеют характерные особенности, связанные с различиями в точности и сложности различных сенсорных технологий.
Серийная неудача
Структурированные пропуски могут возникать из-за сбоев или несоответствий в процессах сбора данных, таких как неисправность датчиков или несоответствие покрытия датчиков, или систематических сбоев в тестировании из-за проблем с пакетами данных. Эти проблемы могут быть как временными, так и неизбежными в процессе сбора данных. Например, данные, полученные от оборудования дистанционного зондирования через спутник, могут не содержать наблюдений в определенное время из-за временных сбоев в работе спутника или быть систематически ограниченными для определенных географических регионов из-за ограничений в орбитах спутников или полях зрения (как это происходит, например, в так называемой "полярной дыре").
Закономерности пропусков
Структурированные пропуски часто возникают в данных опроса в виде закономерностей (Groves, R. M. et al. Survey Methodology (John Wiley & Sons, 2011). Закономерность пропуска возникает, когда набор ответов получается только в том случае, если ответ на предыдущий вопрос - "Да", а ответ "Нет" приводит к тому, что участник переходит к последующей части опроса. В таких случаях большие блоки пропусков возникают как неотъемлемая и ожидаемая особенность плана исследования.
Популяционная неоднородность
Структурированный недостаток возникает при рассмотрении моделей поведения или характеристик человека. Например, люди, естественно, имеют различные интересы и желания, демонстрируют различные модели активности и обладают различными физическими характеристиками. Данные, объединяющие эти модели поведения или характеристики большой популяции, естественно, будут содержать большое количество SM, отражающих присущее данной популяции разнообразие как по внутренним характеристикам, так и по поведению.
Хотя эти примеры не являются исчерпывающими, они подчеркивают некоторые трудности работы с SM. В некоторых случаях SM ожидаются и могут быть уместными; в то время как в других случаях они могут быть связаны как с устранимыми, так и неизбежными недостатками сбора данных и могут сильно помешать последующему обучению. Поэтому понимание и работа с SM не простой процесс: необходим набор инструментов, адаптированных к различным обстоятельствам, а также процессы, с помощью которых исследователи могут развивать эти инструменты по мере развития понимания SM.
Концептуализация SM
В этом разделе рассмотрена литература, посвященная отсутствующим данных, а также освещено, как существующие таксономии не полностью отражают сложность SM. Мы также рассмотрим некоторые общие возможности появления к SM и конкретизируем проблематику на примере реальной базы медицинских данных.
Предположим, что у нас есть матрица данных X размером n × p, которая соответствует n единицам, измеренным по p переменным. Теперь рассмотрим соответствующую n × p индикаторную матрицу R, записи которой равны либо 0, либо 1, так что Rij = 0 означает, что Xij отсутствует, а Rij = 1 означает, что Xij наблюдается. Мы можем разложить X на наблюдаемую (Xobs) и отсутствующую части данных (Xmis) следующим образом:
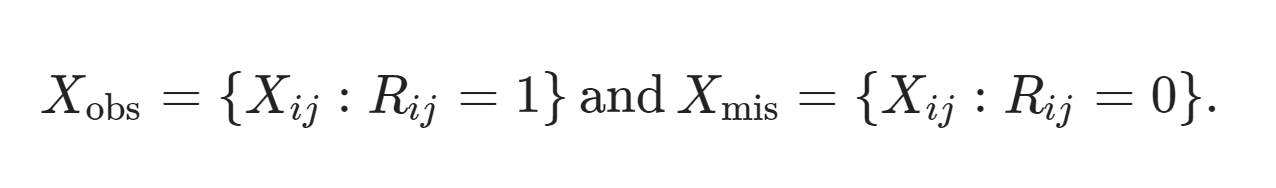
Используя эту терминологию, мы можем определить две важные фундаментальные концепции недостающих данных: (1) механизмы недостающих данных и (2) паттерны недостающих данных.
Механизмы недостающих данных относятся к процессам, посредством которых в данных возникают недостающие значения. В 1976 году Рубин предложил таксономию механизмов отсутствия данных, рассматривая условное распределение p(R ∣ X, ϕ), которое с тех пор было принято в качестве стандарта для классификации механизмов отсутствия данных3. Эта таксономия моделирует вероятность отсутствия значений как функцию переменных в данных, где p( ⋅ ) обозначает общую функциональную форму связи, а ϕ представляет собой параметры в модели, которые определяют точную связь между R и X. В частности, Рубин предложил следующие три класса пропущенных данных:
- (1) данные, отсутствующие полностью случайно (MCAR). В этом случае отсутствующие показания не зависят от наблюдаемых и ненаблюдаемых данных, и нет систематических различий между образцами, по которым имеются отсутствующие данные, и образцами, по которым имеются полные данные. Для данных, которые являются MCAR, анализ полного случая (то есть простое исключение из анализа тех единиц, для которых данные отсутствуют) может ослабить статистическую мощность, но не вносит смещения. Математически, для данных, которые являются MCAR, p(R∣X, ϕ) = p(R∣ϕ).
- (2) Случайные пропуски (MAR). В этом случае отсутствующие показания одной переменной зависят от наблюдений другой. Например, при заполнении анкеты о психическом здоровье мужчины могут быть менее откровенны, чем женщины. Таким образом, при условии, что гендерные данные являются полными, пропуски в данных об ответах будут связаны с наблюдаемой характеристикой. Для данных, которые являются MAR, анализ полных случаев может привести к смещению, поскольку он может выбрать подмножества случаев, которые не являются репрезентативными для данных в целом. Математически, для данных, которые являются MAR, p(R∣X, ϕ) = p(R∣Xobs, ϕ).
- (3) Неслучайные пропуски (MNAR). В этом случае отсутствующие показания в одной переменной зависят от отсутствия в других или от систематических факторов, выходящих за рамки эксперимента или процесса сбора данных. Для данных, которые являются MNAR, анализа полных случаев может внести смещение; более того, поскольку источник этого смещения не очевиден, его нелегко устранить в последующем анализе. Математически, для данных, которые являются MNAR, p(R∣X, ϕ) = p(R∣X, ϕ) (то есть в этом классе не существует упрощающей зависимости).
Паттерны отсутствующих данных характеризуют процессы возникновения расположения отсутствующих значений в данных. Хотя существует множество возможных способов количественной оценки закономерностей, на практике обычно используются две категории: монотонные и немонотонные закономерности (рис. 2 и ссылка 1). Монотонная модель относится к модели, в которой возможно упорядочить переменные p таким образом, когда Rij = 0, Rik = 0 для всех k > j. Немонотонная модель относится к модели, в которой невозможно упорядочить переменные таким образом. Монотонные модели отсутствующих данных обычно позволяют более чисто разложить данные на Xmis и Xobs, что, в свою очередь, может облегчить использование методов, позволяющих получить результаты аналитически1. Однако в многомерных условиях вероятность возникновения немонотонных моделей гораздо выше. Здесь результаты, как правило, могут быть только аппроксимированы с помощью вычислительных методов, таких как методы Марковской цепи Монте-Карло, хотя зачастую эти приближения могут быть очень точными. Несмотря на то, что может показаться, что паттерны отсутствующих данных имеют сходство с механизмами отсутствующих данных, эти два понятия являются разными и отличными характеристиками отсутствующих данных. Например, немонотонные закономерности могут возникать из-за наличия в данных механизмов MCAR, MAR или MNAR, а также сочетания всех трех механизмов. Хотя взаимосвязь между закономерностями и механизмами в целом трудно определить, существуют некоторые простые правила: например, монотонные закономерности вряд ли возникнут в результате механизмов MCAR из-за сложной структурированной формы, которую они обычно принимают.
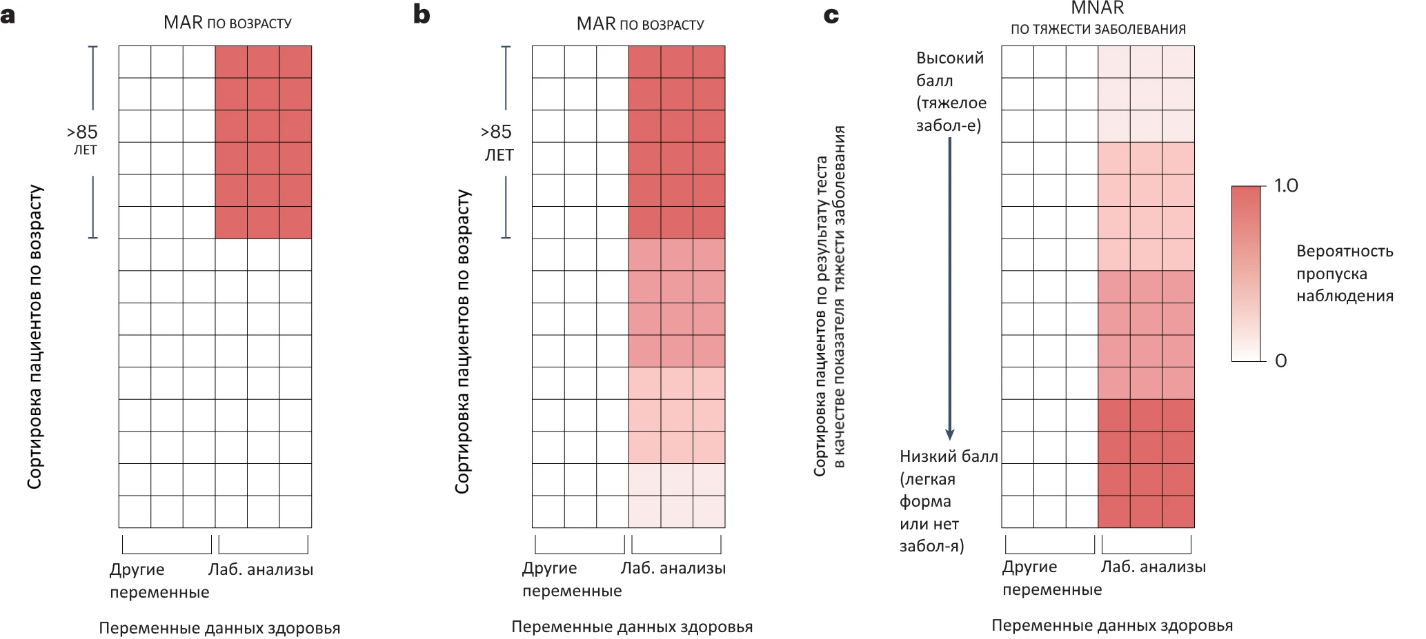
Рис. 2: Примеры SM.
Пропуски могут возникать неявным образом, который плохо учитывается в классической теории.
Например, врач может рекомендовать или не рекомендовать проведение ряда анализов для конкретного пациента в зависимости от состояния его здоровья или других соответствующих характеристик, таких как возраст или пол, что приводит к появлению в данных набора переменных, которые одновременно отсутствуют или наблюдаются. Поскольку решения врачей редко бывают бинарными, результирующие отношения отсутствия могут быть вероятностными, а не определенными, что приводит к набору переменных, которые с большей вероятностью будут отсутствовать совместно. a, Гипотетический сценарий, в котором лабораторные исследования проводятся для всех пациентов моложе критического возраста (здесь 85 лет), но не для тех, кто старше. Это пример монотонной модели отсутствующих данных. b, Более реалистичный сценарий, в котором вероятность проведения теста уменьшается с увеличением возраста пациента. Хотя он представляет аналогичный механизм отсутствия данных (MAR), это приводит к немонотонной модели. c, Ситуация, в которой врач с большей вероятностью назначит диагностическое лабораторное исследование на основании предполагаемого статуса заболевания, который выявляется самим тестом (и поэтому данные являются MNAR), что приводит к немонотонной модели SM. Здесь модель SM показана только для иллюстрации: в действительности модель и структура пропусков были бы ненаблюдаемыми, поскольку они зависят от ненаблюдаемой переменной (балла диагностического теста, который является косвенным показателем скрытой тяжести заболевания).
Механизмы и модели отсутствия данных Рубина важны, поскольку они являются мощным руководством для определения различных типов пропусков; когда такие проблемы, как смещение, могут возникнуть, а когда нет; и когда инструменты (такие как заполнение пропусков/imputation) будут эффективны, а когда нет. В настоящее время существует множество мощных методов работы с отсутствующими данными, предполагающих, что они являются MCAR, включая различные инструменты заполнения пропусков1. С данными MAR работать сложнее, но иногда с ними можно справиться с помощью более сложных инструментов заполнения, таких как многомерное заполнение с помощью цепных уравнений26. Поскольку они наименее точно определены и наиболее сложны, с данными MNAR, справиться еще сложнее, и обычно они рассматриваются очень осторожно и решаются более прагматичными, индивидуальными способами - например, путем ручного исследования и коррекции моделей пропусков или путем проведения анализа чувствительности, чтобы определить, как изменяются результаты анализа при различных вариантах исключения данных или заполнения.
Однако, несмотря на свою несомненную полезность, таксономии Рубина не полностью учитывают многомерные модели SM, которые все чаще встречаются в современных приложениях машинного обучения. Хотя очевидно, что SM связаны с категориями MAR и MNAR Рубина, они не являются исключительно связанными ни с одной из них. Иллюстративный пример приведен на рис. 2. Здесь врач принимает решение о том, каким пациентам назначить серию анализов, либо основываясь исключительно на их возрасте (рис. 2a,b), либо на предполагаемом состоянии заболевания (рис. 2c). В случае, когда решение принимается на основе возраста, данные являются MAR, поскольку возраст полностью наблюдаем. В случае, когда решение принимается на основе статуса заболевания, который неизвестен, данные являются MNAR, и, что важно, структура отсутствующих данных является ненаблюдаемой, поскольку зависит от неизвестной/неочевидной переменной – опасное следствие MNAR. Более того, в зависимости от того, происходит ли тестирование определенным или вероятностным образом (то есть, если врач всегда направляет пациентов определенного возраста на тестирование, как на рис. 2a, или использует свое суждение, основанное на других, возможно, неучтенных характеристиках, как на рис. 2b), результирующие паттерны могут быть монотонными или немонотонными.
В условиях высокой размерности, когда множество различных генеративных механизмов могут накладывать различные паттерны пропусков на данные, такие нюансы могут затруднить обнаружение и характеристику различных типов SM, присутствующих в наборе данных. Например, монотонные паттерны, такие как закономерности блочных пропущенных данных, часто проявляются четкими и очевидными способами, и их легко визуализировать и охарактеризовать. С другой стороны, немонотонные модели, возникающие из-за базовой структуры, в которой отсутствующие значения распределены тонким слоем по многомерному пространству или в условиях MNAR, могут быть гораздо более губительными, их сложнее охарактеризовать или даже обнаружить.
По мере роста интереса к обучению на сложных, высокоразмерных данных, такие закономерности пропусков будут встречаться все чаще. Наивное обучение ML-модели на таких данных представляет опасность, поскольку стандартные методы недостающих данных не позволяют в достаточной степени решить проблемы SM. Например, полный анализ данных на рис. 2a (по умолчанию во многих библиотеках ML) удалит всех пациентов старше 85 лет и тем самым внесет погрешность, отбросив важную часть популяции. С другой стороны, обычно применяемые методы заполнения, такие как множественное заполнение или заполнение на основе деревьев, могут быть либо неуместными, поскольку данные намеренно отсутствуют, либо вносить высокую неопределенность в зависимости от количества отсутствующих переменных и наблюдений. Таким образом, разработка методов расшифровки (часто сложной) геометрии SM имеет решающее значение в таких условиях.
Во вставке 1 описаны некоторые общие пути к SM; в статье приведены примеры проблем, возникающих при работе с SM в сложном реальном наборе данных, представляющим собой лонгитудные данные онкологических пациентов из 280 центров, включая клинические данные, данные геномных анализов и исходы. Такой набор неизбежно включает в себя структурированные пропуски из-за эволюции методов геномных анализов, локальными особенностями назначений, типовыми анализами, присущими определенному типу онкологических заболеваний и т.п. Эти примеры показывают, что SM включает в себя очень широкий спектр явлений, которые не укладываются в существующие категории для моделей или механизмов пропущенных данных, и каждое из них представляет свои собственные проблемы. В сложных, многомерных условиях эти проблемы еще более усугубляются: в данном наборе данных может присутствовать множество различных форм SM, каждая из которых возникает благодаря различным механизмам, каждая демонстрирует свои собственные закономерности, которые могут (или не могут) соотноситься с закономерностями отсутствия данных в других местах. Такое разнообразие препятствует формированию SM как самостоятельной области исследования, и, следовательно, пока не существует теоретических инструментов для классификации различных распространенных форм SM, понимания их последствий для последующего обучения или эффективной борьбы с ними.
На пути к таксономии SM
Приведенные выше примеры показывают, что для получения знаний из больших гетерогенных связанных наборов данных нам нужны новые способы концептуализации SM и инструменты для работы с ними как с интегрированной частью конвейера ML (рис. 1).
С этим связано несколько отдельных математических и вычислительных задач. Во-первых, существующие таксономии не отражают всего богатства SM как явления, и нам не хватает языка для определения и количественной оценки как механизмов, так и моделей структурированных пропусков: необходимы новые математические формулировки, расширяющие и дополняющие классическую таксономию Рубина и рассматривающие SM как фундаментально многомерное явление. Действительно, простое обнаружение и классификация всех различных типов SM, присутствующих в большом многомерном наборе данных, может быть чрезвычайно сложной задачей, и пока для этого не существует инструментов. Во-вторых, не имея формальной основы для количественной оценки SM, мы не располагаем инструментами для оценки того, насколько SM компрометирует или искажает модели машинного обучения. В некоторых случаях отсутствующие данные - даже если они значительны по объему и сильно структурированы - не влияют на эффективность модели. Это может произойти, если, например, отсутствующие данные являются периферийными для интересующего результата или если отсутствующие показания могут быть точно выведены из наблюдений. Однако в других обстоятельствах наличие даже незначительного SM может серьезно ухудшить производительность модели. Это может произойти, если недостающие данные касаются переменной, которая является причинной детерминантой или прогнозируемой для интересующего исхода. Хотя такие вопросы в некоторой степени могут быть решены в каждом конкретном случае, в настоящее время не хватает формальной основы для принципиального решения этих вопросов в целом.
В-третьих, влияние типов SM на последующие выводы и обучение еще недостаточно изучено. Например, если мы предполагаем, что (возможно, неизвестная) связь между переменными и подмножеством этих переменных проявляет SM, какое влияние это оказывает на последующий анализ с участием других переменных?
В-четвертых, мы очень слабо понимаем, как SM влияет на предвзятость и справедливость алгоритмов. В очень чувствительных и/или регулируемых областях (таких как здравоохранение и уголовное правосудие, в которых инструменты ML начинают использоваться) эти проблемы являются первостепенными: необходимо, чтобы любые инструменты ML, разработанные и внедренные для общественного блага, решали вопросы объективным и прозрачным образом (MacArthur, B. D., Dorobantu, C. & Margetts, H. Resilient government requires data science reform. Nat. Hum. Behav. https://doi.org/10.1038/s41562-022-01423-6 (2022)). Для этого нам необходимо лучше понять, как SM влияет на алгоритмическую предвзятость и справедливость решений ML.
Исходя из этих наблюдений, Институт Алана Тьюринга созвал серию семинаров, чтобы сформулировать эти вопросы и определить траекторию будущих исследований в области SM. В результате были сформулированы девять грандиозных задач для SM. Задачи можно сгруппировать в следующие четыре категории (показаны на рис. 1): (1) происхождение и определения SM; (2) измерения и моделирование и SM; (3) выводы и прогнозы и SM; и (4) каузальность и SM. В совокупности они дают представление о масштабе проблем, связанных с SM, обеспечивают "дорожную карту" для развития SM как области исследования и намечают набор будущих направлений исследований, которые помогут продвинуть ML в масштабе.
Перечень сформулированных задач “дорожной карты”:
- Задача 1: Определение SM
- Задача 2: Изучение геометрии SM
- Задача 3: Проектирование экспериментов с использованием SM
- Задача 4: Прогнозирование с помощью SM
- Задача 5: Выводы и оценки с помощью SM
- Задача 6: Заполнение SM
- Задача 7: Сравнение и оценка инструментов SM
- Задача 8: Причинность (каузальность) SM
- Задача 9: Этические последствия SM